Question

Let ${{R}_{0}}$ be the set of all non-zero real numbers.
Show that $f:{{R}_{0}}\to {{R}_{0}}:f(x)=\dfrac{1}{x}$ is a one-one onto function.

Answer 1

Hint: To check whether the given function is one-one or not, assume two elements ${{x}_{1}}\text{ and }{{x}_{2}}$ in the set of the domain of the given function and substitute $f({{x}_{1}})=f({{x}_{2}})$. If ${{x}_{1}}={{x}_{2}}$, then $f(x)$ is one-one and if there is any more relation between ${{x}_{1}}\text{ and }{{x}_{2}}$ other than ${{x}_{1}}={{x}_{2}}$ then $f(x)$ is not one-one. To check whether the given function is onto or not, check if the range of $f(x)$ is equal to co-domain or not. Here, co-domain is the set of all values of $f(x)$ in which the range of the function is constrained.

Complete step-by-step solution -
It is given that function is defined for all real numbers except 0 and over all real numbers except 0. Therefore, both domain and co-domain of the given function consists of the set of all real numbers except 0.
First let us show the function is one-one.
Assume two elements ${{x}_{1}}\text{ and }{{x}_{2}}$ in the set of the domain of the given function. Therefore,
$f({{x}_{1}})=f({{x}_{2}})$
Substituting, ${{x}_{1}}\text{ and }{{x}_{2}}$ in the function, we get,
$\begin{aligned} & \dfrac{1}{{{x}_{1}}}=\dfrac{1}{{{x}_{2}}} \\\ & \Rightarrow \dfrac{1}{{{x}_{1}}}-\dfrac{1}{{{x}_{2}}}=0 \\\ \end{aligned}$
Taking L.C.M we get,
$\dfrac{{{x}_{2}}-{{x}_{1}}}{{{x}_{1}}{{x}_{2}}}=0$
By cross-multiplication we get,
$\begin{aligned} & {{x}_{2}}-{{x}_{1}}=0 \\\ & {{x}_{2}}={{x}_{1}} \\\ \end{aligned}$
Clearly, we can see that, when $f({{x}_{1}})=f({{x}_{2}})$ then, ${{x}_{1}}={{x}_{2}}$. Therefore, $f(x)$ is one-one.
Now, let us show that the given function is onto by graphical method.

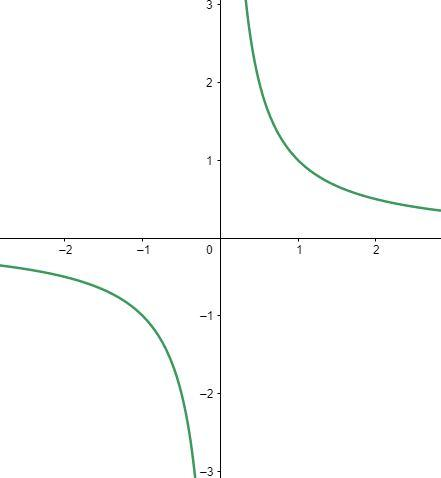
Clearly, we can see that the range of the function $f(x)=\dfrac{1}{x}$ extends from $-\infty \text{ to }\infty$. Therefore, the range of the given function is all real numbers except 0. Hence, range and codomain of the function are equal.
Therefore, it is proved that $f(x)$ is onto.

Note: One may note that we do not have to cancel the common terms while checking whether the function is one-one or not. Consider all the possible relations between ${{x}_{1}}\text{ and }{{x}_{2}}$ and then only come to the conclusion just as we did in the above solution. We have used the graphical method to show whether the given function is onto or not because it is easy for anyone to draw the graph.