Question

Let p(x) = $x^5 + x^2 + 1$ have roots $x_1, x_2, x_3, x_4$ and $x_5$, $g(x) = x^2 -2$, then the value of $g(x_1)g(x_2)g(x_3)g(x_4)g(x_5) - 30g(x_1x_2x_3x_4x_5)$, is 62

Answer 1

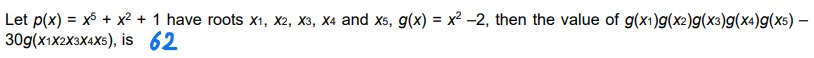
53

Answer 2

Let $p(x) = x^5 + x^2 + 1$ with roots $x_1, x_2, x_3, x_4, x_5$. Let $g(x) = x^2 - 2$. We need to find the value of the expression $E = g(x_1)g(x_2)g(x_3)g(x_4)g(x_5) - 30g(x_1x_2x_3x_4x_5)$.

First, let's find the product of the roots $x_1x_2x_3x_4x_5$. For a polynomial $a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0$, the product of the roots is $(-1)^n \frac{a_0}{a_n}$. For $p(x) = x^5 + 0x^4 + 0x^3 + x^2 + 0x + 1$, the degree is $n=5$, the constant term is $a_0=1$, and the leading coefficient is $a_5=1$. The product of the roots is $x_1x_2x_3x_4x_5 = (-1)^5 \frac{1}{1} = -1$.

Now, let's evaluate the second term of the expression $E$: $30g(x_1x_2x_3x_4x_5)$. This is $30g(-1)$. $g(-1) = (-1)^2 - 2 = 1 - 2 = -1$. So, the second term is $30(-1) = -30$.

Next, let's evaluate the first term: $g(x_1)g(x_2)g(x_3)g(x_4)g(x_5) = \prod_{i=1}^5 g(x_i)$. $g(x_i) = x_i^2 - 2$. So the first term is $\prod_{i=1}^5 (x_i^2 - 2)$. Let $y_i = x_i^2$. We need to evaluate $\prod_{i=1}^5 (y_i - 2)$.

The roots $x_i$ satisfy $p(x_i) = x_i^5 + x_i^2 + 1 = 0$. $x_i^5 = -(x_i^2 + 1)$. Squaring both sides, we get $(x_i^5)^2 = (-(x_i^2 + 1))^2$, which simplifies to $x_i^{10} = (x_i^2 + 1)^2 = x_i^4 + 2x_i^2 + 1$. Let $y = x^2$. Then $y_i = x_i^2$. Substituting $x_i^2 = y_i$ and $x_i^{10} = (x_i^2)^5 = y_i^5$, $x_i^4 = (x_i^2)^2 = y_i^2$, the equation becomes $y_i^5 = y_i^2 + 2y_i + 1$. So, $y_i$ is a root of the polynomial $q(y) = y^5 - y^2 - 2y - 1$. The roots of $q(y)$ are $y_1 = x_1^2, y_2 = x_2^2, y_3 = x_3^2, y_4 = x_4^2, y_5 = x_5^2$. Thus, $q(y) = (y-y_1)(y-y_2)(y-y_3)(y-y_4)(y-y_5)$.

The first term we need to evaluate is $\prod_{i=1}^5 (y_i - 2) = (y_1-2)(y_2-2)(y_3-2)(y_4-2)(y_5-2)$. This is equal to $q(2)$. $q(2) = (2)^5 - (2)^2 - 2(2) - 1 = 32 - 4 - 4 - 1 = 32 - 9 = 23$. So, the first term is 23.

Now we can calculate the value of the expression $E$: $E = (\text{first term}) - (\text{second term})$ $E = 23 - (-30) = 23 + 30 = 53$.