Question

Let $P(x) = x^{32} – x^{25} + x^{18} – x^{11} + x^4 - x^3 + 1$. Which of the following are CORRECT ?

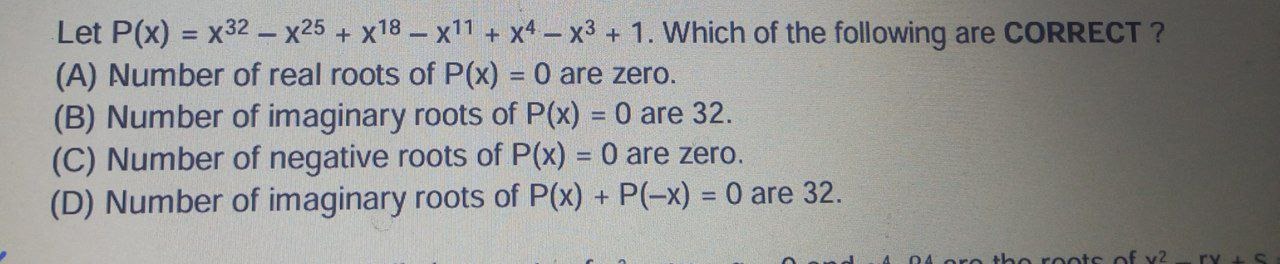
• A. Number of real roots of P(x) = 0 are zero.
• B. Number of imaginary roots of P(x) = 0 are 32.
• C. Number of negative roots of P(x) = 0 are zero.
• D. Number of imaginary roots of P(x) + P(-x) = 0 are 32.

Answer 1

Answer: (A), (B), (C), (D)

A, B, C, D

Answer 2

To determine the correctness of the given statements, we will analyze the polynomial $P(x) = x^{32} – x^{25} + x^{18} – x^{11} + x^4 - x^3 + 1$.

Analysis of P(x) = 0:

1. Number of negative roots of P(x) = 0 (Statement C):

To find the number of negative real roots, we examine $P(-x)$. $P(-x) = (-x)^{32} – (-x)^{25} + (-x)^{18} – (-x)^{11} + (-x)^4 - (-x)^3 + 1$ $P(-x) = x^{32} + x^{25} + x^{18} + x^{11} + x^4 + x^3 + 1$

All coefficients in $P(-x)$ are positive. According to Descartes' Rule of Signs, the number of negative real roots of $P(x)$ is equal to the number of sign changes in $P(-x)$. Since there are no sign changes in $P(-x)$, there are zero negative real roots for $P(x)=0$.

Alternatively, for any real $x < 0$, let $x = -t$ where $t > 0$. Then $P(x) = P(-t) = t^{32} + t^{25} + t^{18} + t^{11} + t^4 + t^3 + 1$. Since $t > 0$, all terms are positive, so $P(-t) > 0$. Thus, $P(x) > 0$ for all $x < 0$. This confirms there are no negative real roots.

Therefore, statement (C) is CORRECT.

2. Number of positive roots of P(x) = 0:

Let's analyze $P(x)$ for $x \ge 0$.

• For $x=0$, $P(0) = 1 \ne 0$. So $x=0$ is not a root.
• For $0 < x < 1$:

We can group the terms as: $P(x) = x^{32} + (x^{18} - x^{25}) + (x^4 - x^{11}) + (1 - x^3)$ $P(x) = x^{32} + x^{18}(1 - x^7) + x^4(1 - x^7) + (1 - x^3)$

For $0 < x < 1$: $x^{32} > 0$ $1 - x^7 > 0 \implies x^{18}(1 - x^7) > 0$ $1 - x^7 > 0 \implies x^4(1 - x^7) > 0$ $1 - x^3 > 0$

Since all terms are positive, $P(x) > 0$ for $0 < x < 1$.

• For $x \ge 1$:

We can group the terms as: $P(x) = (x^{32} - x^{25}) + (x^{18} - x^{11}) + (x^4 - x^3) + 1$ $P(x) = x^{25}(x^7 - 1) + x^{11}(x^7 - 1) + x^3(x - 1) + 1$

For $x \ge 1$: $x^7 - 1 \ge 0 \implies x^{25}(x^7 - 1) \ge 0$ $x^7 - 1 \ge 0 \implies x^{11}(x^7 - 1) \ge 0$ $x - 1 \ge 0 \implies x^3(x - 1) \ge 0$

The constant term is $1 > 0$. Since all terms are non-negative and the constant term is positive, $P(x) \ge 1$ for $x \ge 1$. Combining these results, $P(x) > 0$ for all real $x \ge 0$. Thus, there are no positive real roots.

3. Number of real roots of P(x) = 0 (Statement A):

Since there are no negative real roots, no positive real roots, and $P(0) \ne 0$, the total number of real roots of $P(x) = 0$ is zero. Therefore, statement (A) is CORRECT.

4. Number of imaginary roots of P(x) = 0 (Statement B):

The degree of the polynomial $P(x)$ is 32. By the Fundamental Theorem of Algebra, a polynomial of degree $n$ has exactly $n$ roots in the complex numbers (counting multiplicity). Since $P(x)$ has degree 32, it has 32 roots in total. We found that the number of real roots is 0. Therefore, the number of imaginary (non-real complex) roots is $32 - 0 = 32$. Therefore, statement (B) is CORRECT.

Analysis of P(x) + P(-x) = 0 (Statement D):

Let $Q(x) = P(x) + P(-x)$. $Q(x) = (x^{32} – x^{25} + x^{18} – x^{11} + x^4 - x^3 + 1) + (x^{32} + x^{25} + x^{18} + x^{11} + x^4 + x^3 + 1)$ $Q(x) = 2x^{32} + 2x^{18} + 2x^4 + 2$ $Q(x) = 2(x^{32} + x^{18} + x^4 + 1)$

We need to find the number of imaginary roots of $Q(x) = 0$, which is equivalent to finding roots of $x^{32} + x^{18} + x^4 + 1 = 0$. Let $f(x) = x^{32} + x^{18} + x^4 + 1$. The degree of $f(x)$ is 32, so it has 32 roots in total.

Let's check for real roots of $f(x) = 0$:

• If $x \ge 0$: $x^{32} \ge 0$, $x^{18} \ge 0$, $x^4 \ge 0$. So, $f(x) = x^{32} + x^{18} + x^4 + 1 \ge 0 + 0 + 0 + 1 = 1$. Thus, $f(x) \ge 1$ for all $x \ge 0$. So, no positive real roots and $x=0$ is not a root.
• If $x < 0$: $x^{32} > 0$ (even power), $x^{18} > 0$ (even power), $x^4 > 0$ (even power). So, $f(x) = x^{32} + x^{18} + x^4 + 1 > 0 + 0 + 0 + 1 = 1$. Thus, $f(x) > 1$ for all $x < 0$. So, no negative real roots.

Since $f(x) \ge 1$ for all real $x$, $f(x) = 0$ has no real roots. As the total number of roots is 32 and the number of real roots is 0, the number of imaginary roots of $Q(x) = 0$ is $32 - 0 = 32$. Therefore, statement (D) is CORRECT.

All statements (A), (B), (C), and (D) are correct.