Question

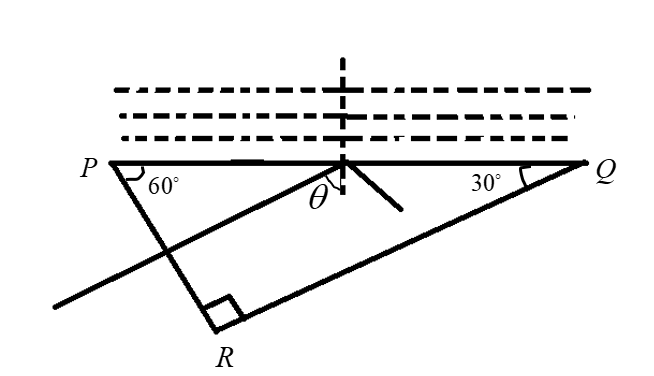
Let PQR is a right-angled prism with other angles as ${60^0}$ and ${\text{ }}{30^0}$. PQ has a thin layer of liquid and light falls normally on the face PR as shown in the figure. If the refractive index of the prism is $1.5$, then for total internal reflection, the maximum refractive index of liquid will be

A) $1.2$
B) $1.3$
C) $1.4$
D) $1.5$

Answer 1

We know that whenever a change in the medium there change in velocity of light takes place. This is because of the refractive index of the medium.

Complete step by step answer:
Given, refractive index of the prism = $1.5$
When light travels from an optically denser medium to a rarer medium, at the interface, under certain conditions, light is totally reflected back into the denser medium. This phenomenon is called total internal reflection. For a pair of given media, the angle of the incident in the denser medium for which the angle of refraction in the rarer medium becomes ${90^0}$ is called critical angle (C).

If the angle of incidence is greater than the critical angle C for the ray OD, then the ray of light is reflected back completely into the denser medium. This phenomenon is called total internal reflection.
For total internal reflection, at PQ
$\Rightarrow \theta > C$
From the geometry of the figure, $\theta = {60^0}{\text{ }}(\because corresponding{\text{ }}angle)$
Then, ${60^0} > C$
$\Rightarrow \sin 60 > \sin C$
$\Rightarrow \dfrac{{\sqrt 3 }}{2} > \dfrac{{{n_{liquid}}}}{{{n_{prism}}}}$
$\Rightarrow {n_{liquid}} < \dfrac{{\sqrt 3 }}{2} \times {n_{prism}}$
$\Rightarrow {n_{liquid}} < \dfrac{{\sqrt 3 }}{2} \times 1.5$
$\therefore {n_{liquid}} < 1.3$

Therefore, the correct option is (B).

Additional information:
A) The phenomenon of bending of a ray of light when it travels from one medium to another of different optical density is known as refraction of light.
B) The phenomenon in which light travelling in one medium, incident on the surface of another returns to the first medium is called reflection of light.
C) The refractive index of a medium is a measure of the velocity of light in the medium. The greater the refractive index of a medium, the smaller is the velocity of light in that medium and vice versa. A medium that has a higher refractive index is called an optically denser medium and the one that has a smaller refractive index is said to be an optically rarer medium.
D) Relation between the critical angle and refractive index:
Let ${n_2}$ be the refractive index of a denser medium and ${n_1}$ be the refractive index of the rarer medium.
When $i = C$, $r = {90^0}$.
$\therefore$ According to Snell’s law, we have,
${n_2}\sin C = {n_1}\sin {90^0}$
$\dfrac{{{n_2}}}{{{n_1}}} = \dfrac{1}{{\sin C}}$
$\therefore {n_{21}} = \dfrac{1}{{\sin C}}$
Where ${n_{21}}$ is the refractive index of the denser medium with respect to that of the rarer medium.

Note:
An alternative method for this problem is
Let the refractive index of the prism be ${n_p}$ and that of liquid be ${n_l}$.
Now from the figure, the angle of incidence inside the prism is ${60^0}$ . if this is the critical angle for prism and liquid interface then,
$\Rightarrow {n_{pl}} = \dfrac{1}{{\sin C}}$
$\Rightarrow \dfrac{{{n_p}}}{{{n_l}}} = \dfrac{1}{{\sin C}}$
But $C = {60^ \circ }$
$\Rightarrow {n_l} = {n_p}$
Substituting the values we get,
$\Rightarrow \sin C = 1.5\sin {60^0}$
$\Rightarrow 1.2999$
$\therefore 1.3$