Question

Let PQR be a triangle of area $\Delta$ with $a = 2$ , $b = \dfrac{7}{2}$ and $c = \dfrac{5}{2}$ , where a, b and c are the lengths of the sides of the triangle opposite to the angles at P, Q and R respectively. Then $\dfrac{{2\sin P - \sin 2P}}{{2\sin P + \sin 2P}}$ equals
A $\dfrac{3}{{4\Delta }}$
B $\dfrac{{45}}{{4\Delta }}$
C ${\left( {\dfrac{3}{{4\Delta }}} \right)^2}$
D ${\left( {\dfrac{{45}}{{4\Delta }}} \right)^2}$

Answer 1

Hint : We know that the area of a triangle is defined as the total region that is enclosed by the three sides of any particular triangle and basically, it is equal to half of the base times height and here a, b, c are the sides of a triangle PQR with given lengths opposite to the angles at P, Q and R, in which we can find $\dfrac{{2\sin P - \sin 2P}}{{2\sin P + \sin 2P}}$ by applying trigonometric identities with respect to sin function.
Formula used:
$s = \dfrac{{a + b + c}}{2}$
s is the sum of the given lengths of sides of a triangle.
a, b, c are the given lengths of sides of a triangle.

Complete step-by-step answer :
Let us write the given data:
PQR be a triangle of area $\Delta$
$a = 2$ , $b = \dfrac{7}{2}$ and $c = \dfrac{5}{2}$

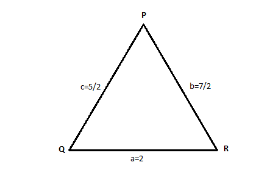
Where a, b and c are the lengths of the sides of the triangle opposite to the angles at P, Q and R respectively, hence we need to find $\dfrac{{2\sin P - \sin 2P}}{{2\sin P + \sin 2P}}$ .
According to the given data we have:
$a = 2$ = QR
$b = \dfrac{7}{2}$ = PR
$c = \dfrac{5}{2}$ = PQ
Let us find the sum of all the three lengths a, b, c as
$s = \dfrac{{a + b + c}}{2}$
$s = \dfrac{{2 + \left( {\dfrac{7}{2}} \right) + \left( {\dfrac{5}{2}} \right)}}{2}$
Simplifying the terms, we get:
$s = \dfrac{8}{2} = 4$
Now let us find,
$\dfrac{{2\sin P - \sin 2P}}{{2\sin P + \sin 2P}}$ ………………… 1
We know that,
$\sin 2x = 2\sin x\cos x$
Hence let us apply this formula in equation 1
= $\dfrac{{2\sin P - 2\sin P\cos P}}{{2\sin P + 2\sin P\cos P}}$
= $\dfrac{{2\sin P\left( {1 - \cos P} \right)}}{{2\sin P\left( {1 + \cos P} \right)}}$
= $\dfrac{{\left( {1 - \cos P} \right)}}{{\left( {1 + \cos P} \right)}}$
Which is written as:
$\dfrac{{\left( {1 - \cos P} \right)}}{{\left( {1 + \cos P} \right)}}$ = $\dfrac{{2{{\sin }^2}\dfrac{P}{2}}}{{2{{\cos }^2}\dfrac{P}{2}}}$
$\Rightarrow$ $\dfrac{{2{{\sin }^2}\dfrac{P}{2}}}{{2{{\cos }^2}\dfrac{P}{2}}} = {\tan ^2}\dfrac{P}{2}$
We know that,
$\tan \dfrac{P}{2} = \sqrt {\dfrac{{\left( {s - b} \right)\left( {s - c} \right)}}{{s\left( {s - a} \right)}}}$
$\Rightarrow$ ${\tan ^2}\dfrac{P}{2} = \dfrac{{\left( {s - b} \right)\left( {s - c} \right)}}{{s\left( {s - a} \right)}}$
Hence, we get
$\dfrac{{\left( {s - b} \right)\left( {s - c} \right)}}{{s\left( {s - a} \right)}} = \dfrac{{{{\left( {s - b} \right)}^2}{{\left( {s - c} \right)}^2}}}{{{\Delta ^2}}}$
Since,
$\Delta = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)}$
Hence, substitute the values of a, b and c as:
$\dfrac{{{{\left( {s - b} \right)}^2}{{\left( {s - c} \right)}^2}}}{{{\Delta ^2}}}$
$\Rightarrow$ $\dfrac{{{{\left( {4 - \dfrac{7}{2}} \right)}^2}{{\left( {4 - \dfrac{5}{2}} \right)}^2}}}{{{\Delta ^2}}}$
Therefore, after simplifying the terms we get
$\Rightarrow$ ${\left( {\dfrac{3}{{4\Delta }}} \right)^2}$
Hence, option C is the right answer.
So, the correct answer is “Option C”.

Note : We have seen that the area of special triangles could be obtained using the triangle formula. However, for a triangle with the length of sides being given, we can easily find the sum of all the lengths using the formula and to solve the given function we must know all the trigonometric identity functions with respect to the sine, cos and tan functions.