Question

Let PQ be a chord of the parabola ${{y}^{2}}=4x$. A circle drawn with PQ as a diameter passes through the vertex V of the parabola. If Area of $\Delta PVQ$ = 20 $uni{{t}^{2}}$ then the co – ordinates of P are
(a)(-16, -8)
(b)(-16, 8)
(c)(16, -8)
(d)(16, 8)

Answer 1

Hint: Suppose points P and Q as $\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $\left( at_{2}^{2},2a{{t}_{2}} \right)$ by using the parametric coordinates for ${{y}^{2}}=4ax$ (put, a= 1). Angle formed in a semi – circle is ${{90}^{\circ }}$ i.e. angle at vertex by PQ (diameter) is ${{90}^{\circ }}$. So, PV and VQ will be perpendicular to each other. Use area of triangle as,
$=\dfrac{1}{2}\times$ base $\times$ height

Complete step-by-step answer:
Use following results to solve the problem further: -
Product of slopes of two perpendicular lines is -1 and the distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as
$=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$

Given equation of parabola in the problem is,
${{y}^{2}}=4x-(1)$
We know PQ is a chord of the parabola ${{y}^{2}}=4ax$ and a circle is drawn with PQ as a diameter and circle is passing through the vertex V of the parabola.
We know ${{y}^{2}}=4ax$ is symmetric about the x – axis with vertex as (0, 0). So, the coordinate of point V is (0, 0).
So, we can draw diagram with the help of given information as: -

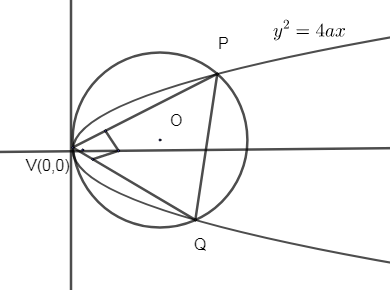
As we know, the angle formed in a semi – circle is ${{90}^{\circ }}$. i.e. angle formed by diameter is ${{90}^{\circ }}$. As PQ is a diameter of the circle with center O in the diagram, so $\angle PVQ={{90}^{\circ }}$ as per the property of the semi – circle.
So, we know area of triangle is given as,
$=\dfrac{1}{2}\times$ base $\times$ height – (2)
Hence, area of $\Delta PVQ$,
$=\dfrac{1}{2}\times \left( PV \right)\times \left( VQ \right)-(3)$
Let us suppose the coordinates of points P and Q on the parabola ${{y}^{2}}=4x$ are $\left( t_{1}^{2},2{{t}_{1}} \right)$ and $\left( t_{2}^{2},2{{t}_{2}} \right)$ [We know the parametric coordinates for ${{y}^{2}}=4x$ are $\left( a{{t}^{2}},2at \right)$].
As VP and VQ are perpendicular to each other, it means the product of slopes of them will be -1, because of the relation.
Product of slopes of two perpendicular lines = -1. – (4)
We know slope of a line with the help of two coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by relation,
Slope $=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}-(5)$
Hence, slope of VP $=\dfrac{2{{t}_{1}}-0}{t_{1}^{2}-0}=\dfrac{2{{t}_{1}}}{t_{1}^{2}}$
Slope of VP $=\dfrac{2}{{{t}_{1}}}$
Similarly, slope of VQ $=\dfrac{2}{{{t}_{2}}}$
Hence, we get from equation (4) as,

& \dfrac{2}{{{t}_{1}}}\times \dfrac{2}{{{t}_{2}}}=-1 \\\ & {{t}_{1}}{{t}_{2}}=-4-(6) \\\ \end{aligned}$$ Now, we need to calculate the distances VP and VQ to get the area from the relation (3). We know the distance between two points $$\left( {{x}_{1}},{{y}_{1}} \right)$$ and $$\left( {{x}_{2}},{{y}_{2}} \right)$$ can be given by distance formula as, $$=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}-(7)$$ Hence, length of VP $$\begin{aligned} & VP=\sqrt{{{\left( 2{{t}_{1}}-0 \right)}^{2}}+{{\left( t_{1}^{2}-0 \right)}^{2}}} \\\ & VP=\sqrt{4t_{1}^{2}+t_{1}^{4}}-(8) \\\ \end{aligned}$$ Similarly, length of VQ $$\begin{aligned} & VQ=\sqrt{{{\left( 2{{t}_{2}}-0 \right)}^{2}}+{{\left( t_{2}^{2}-0 \right)}^{2}}} \\\ & VQ=\sqrt{4t_{2}^{2}+t_{2}^{4}}-(9) \\\ \end{aligned}$$ Now, we know area of $$\Delta PVQ$$ can be given from the equations (3), (8) and (9) as, Area of $$\Delta PVQ$$ $$=\dfrac{1}{2}\times \sqrt{4t_{1}^{2}+t_{1}^{4}}\times \sqrt{4t_{2}^{2}+t_{2}^{4}}$$ Area of $$\Delta PVQ$$ $$=\dfrac{1}{2}\times \sqrt{\left( 4t_{1}^{2}+t_{1}^{4} \right)\left( 4t_{2}^{2}+t_{2}^{4} \right)}$$ Area of $$\Delta PVQ$$ $$=\dfrac{1}{2}\times \sqrt{16t_{1}^{2}t_{2}^{2}+4t_{1}^{2}t_{1}^{4}+4t_{1}^{4}t_{2}^{2}+t_{1}^{4}t_{2}^{4}}$$ Put, $${{t}_{1}}{{t}_{2}}=-4$$, from the equation (6). We get, Area of $$\Delta PVQ$$ = $$\dfrac{1}{2}\sqrt{16\times {{\left( -4 \right)}^{2}}+4t_{1}^{2}t_{2}^{2}\left( t_{2}^{2}+t_{1}^{2} \right)+{{\left( -4 \right)}^{4}}}$$ Area of $$\Delta PVQ$$ $$=\dfrac{1}{2}\sqrt{256+4\times {{\left( -4 \right)}^{2}}\left( t_{1}^{2}+t_{2}^{2} \right)+256}$$ Area of $$\Delta PVQ$$ $$=\dfrac{1}{2}\sqrt{512+64\left( t_{1}^{2}+t_{2}^{2} \right)}$$ We know the area of $$\Delta PVQ$$ from the problem as 20 square units. So, we get, $$\begin{aligned} & 20=\dfrac{1}{2}\sqrt{512+64\left( t_{1}^{2}+t_{2}^{2} \right)} \\\ & 40=\sqrt{512+64\left( t_{1}^{2}+t_{2}^{2} \right)} \\\ \end{aligned}$$ Squaring both sides of the above equation, we get, $$\begin{aligned} & 1600=512+64\left( t_{1}^{2}+t_{2}^{2} \right) \\\ & \dfrac{1600-512}{64}=t_{1}^{2}+t_{2}^{2} \\\ & \dfrac{1088}{64}=t_{1}^{2}+t_{2}^{2} \\\ & 17=t_{1}^{2}+t_{2}^{2} \\\ \end{aligned}$$ Put, $${{t}_{2}}=\dfrac{-4}{{{t}_{1}}}$$ from the equation (6). We get, $$\begin{aligned} & 17=t_{1}^{2}+{{\left( \dfrac{-4}{{{t}_{1}}} \right)}^{2}} \\\ & 17=t_{1}^{2}+\dfrac{16}{t_{1}^{2}} \\\ \end{aligned}$$ Adding 8 to both sides, we get, $$\begin{aligned} & 17+8=t_{1}^{2}+\dfrac{16}{t_{1}^{2}}+8 \\\ & 25={{\left( {{t}_{1}} \right)}^{2}}+{{\left( \dfrac{4}{{{t}_{1}}} \right)}^{2}}+2\times \dfrac{4}{{{t}_{1}}}\times {{t}_{1}} \\\ \end{aligned}$$ So, we get, $${{\left( {{t}_{1}}+\dfrac{4}{{{t}_{1}}} \right)}^{2}}=25$$ Taking square root to both sides, we get, $${{t}_{1}}+\dfrac{4}{{{t}_{1}}}=5$$ or $${{t}_{1}}+\dfrac{4}{{{t}_{1}}}=-5$$ Case 1: $${{t}_{1}}+\dfrac{4}{{{t}_{1}}}=5$$ $$\begin{aligned} & t_{1}^{2}+4=5{{t}_{1}} \\\ & t_{1}^{2}-5{{t}_{1}}+4=0 \\\ & {{t}_{1}}-4{{t}_{1}}-{{t}_{1}}+4=0 \\\ & {{t}_{1}}\left( {{t}_{1}}-4 \right)-1\left( {{t}_{1}}-4 \right)=0 \\\ & \left( {{t}_{1}}-1 \right)\left( {{t}_{1}}-4 \right)=0 \\\ \end{aligned}$$ $${{t}_{1}}=1$$ or $${{t}_{1}}=4$$ Case 2: $${{t}_{1}}+\dfrac{4}{{{t}_{1}}}=-5$$ $$\begin{aligned} & t_{1}^{2}+4=-5{{t}_{1}} \\\ & t_{1}^{2}+5{{t}_{1}}+4=0 \\\ & {{t}_{1}}+4{{t}_{1}}+{{t}_{1}}+4=0 \\\ & {{t}_{1}}\left( {{t}_{1}}+4 \right)+1\left( {{t}_{1}}+4 \right)=0 \\\ & \left( {{t}_{1}}+1 \right)\left( {{t}_{1}}+4 \right)=0 \\\ \end{aligned}$$ Hence, coordinates of P, for case 1 are given as $$\left( t_{1}^{2},2{{t}_{1}} \right)$$. Case 1: $${{t}_{1}}=1$$ Coordinates are (1, 2) Or $${{t}_{1}}=4$$ Coordinates are (16, 8) Case 2: $${{t}_{1}}=-1$$ Coordinates are (1, -2) Or $${{t}_{1}}=-4$$ Coordinates are (16, -8) Hence options (c) and (d) are the possible coordinates of B. Note: One may use the direct result that if two points are subtending a right angle at vertex (0, 0) then, $${{t}_{1}}{{t}_{2}}=-4$$. Where points $$\left( at_{1}^{2},2a{{t}_{1}} \right)$$ and $$\left( at_{2}^{2},2a{{t}_{2}} \right)$$ for the parabola, $${{y}^{2}}=4ax$$. Another approach for the question would be that we can use formula for calculating area of triangle in terms of the coordinates as $$=\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\\ {{x}_{2}} & {{y}_{2}} & 1 \\\ {{x}_{3}} & {{y}_{3}} & 1 \\\ \end{matrix} \right|$$ Where $$\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$$ are coordinates of vertices of any triangle.