Question

Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius $r$. If PS and RQ intersect at a point X on the circumference of the circle, then $2r$ equals
A.$\sqrt {PQ.RS}$
B.$\dfrac{{PQ + RS}}{2}$
C.$\dfrac{{2PQ.RS}}{{PQ + RS}}$
D.$\sqrt {\dfrac{{P{Q^2} + R{S^2}}}{2}}$

Answer 1

Here we will use the trigonometric functions to find the value of $2r$. First, we will draw a rough diagram from the given data. We will use the trigonometric function to get the relation between the diameter of the circle and the tangents. Then we will use the information given in question to get the required condition.

Complete step-by-step answer:
It is given that PQ and RS are the tangents to the circle and PR is the diameter of the circle and $r$ is the radius of the circle.
First, we will draw a figure from the given data. Therefore, we get

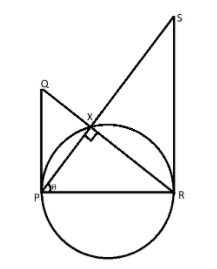
Now we can see that two triangles are formed in the figure.
In the triangle $\Delta PSR$ we will use the trigonometric function to get the relation between PR and RS. Therefore, we get
$\tan \theta = \dfrac{{{\rm{perpendicular}}}}{{{\rm{base}}}} = \dfrac{{RS}}{{PR}}$……………………$\left( 1 \right)$
In the triangle $\Delta PQR$ we will use the trigonometric function to get the relation between PR and PQ. Therefore, we get
$\tan \left( {\dfrac{\pi }{2} - \theta } \right) = \dfrac{{{\rm{perpendicular}}}}{{{\rm{base}}}} = \dfrac{{PQ}}{{PR}}$
We know that $\tan \left( {\dfrac{\pi }{2} - \theta } \right)$ is equal to $\cot \theta$. Therefore, we get
$\Rightarrow \cot \theta = \dfrac{{PQ}}{{PR}}$……………………$\left( 2 \right)$
Now, we will combine equation $\left( 1 \right)$ and equation $\left( 2 \right)$ to get the required condition. Therefore, we get
$\tan \theta \times \cot \theta = \dfrac{{RS}}{{PR}} \times \dfrac{{PQ}}{{PR}}$
We know that $\cot \theta$is the reciprocal of $\tan \theta$. Therefore, we get
$\Rightarrow \tan \theta \times \dfrac{1}{{\tan \theta }} = \dfrac{{RS}}{{PR}} \times \dfrac{{PQ}}{{PR}}$
$\Rightarrow 1 = \dfrac{{PQ.RS}}{{{{\left( {PR} \right)}^2}}}$
On cross multiplying, we get
$\Rightarrow {\left( {PR} \right)^2} = PQ \cdot RS$
Taking square root on both the sides, we get
$\Rightarrow PR = \sqrt {PQ.RS}$
We know that PR is the diameter of the circle and diameter is equal to twice the radius of the circle. Therefore, we get
$\Rightarrow 2r = \sqrt {PQ.RS}$
Hence, $2r$ is equal to $\sqrt {PQ.RS}$.
So, option A is the correct option.

Note: In order to solve this question, we need to use the trigonometric function to get the required condition. Trigonometric function gives the relation between the sides of the right triangle. We should know that tangents are the line segment which only touches the circle at a single point at its circumference.