Question
Question: Let $\phi(x) = (f(x))^3-3(f(x))^2 + 4f(x) + 5x + 3 \sin x + 4 \cos x \forall x \in R$, where $f(x)$ ...
Let ϕ(x)=(f(x))3−3(f(x))2+4f(x)+5x+3sinx+4cosx∀x∈R, where f(x) is a differentiable function ∀x∈R, then
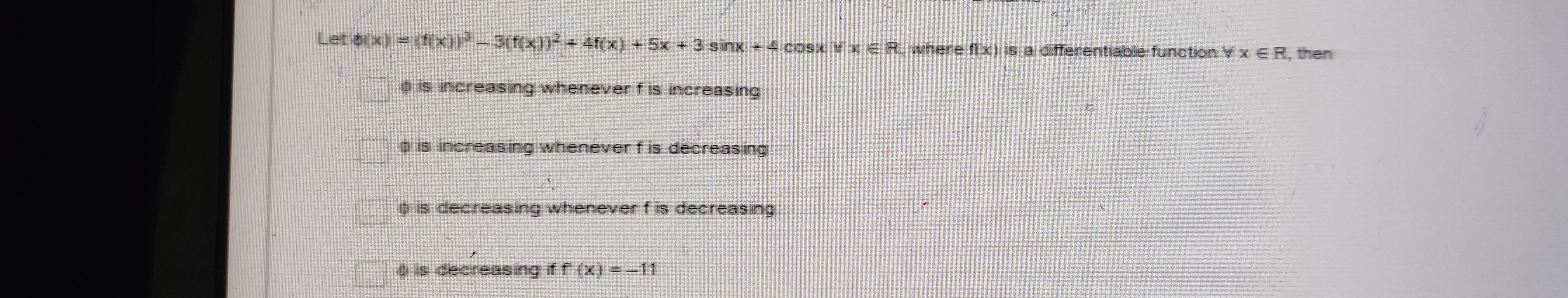
ϕ is increasing whenever f is increasing
ϕ is increasing whenever f is decreasing
ϕ is decreasing whenever f is decreasing
ϕ is decreasing if f′(x)=−11
ϕ is increasing whenever f is increasing, ϕ is decreasing if f′(x)=−11
Solution
Let ϕ(x)=(f(x))3−3(f(x))2+4f(x)+5x+3sinx+4cosx.
To determine when ϕ(x) is increasing or decreasing, we need to find its derivative ϕ′(x).
Using the chain rule and differentiation rules, we get:
ϕ′(x)=dxd((f(x))3)−3dxd((f(x))2)+4dxd(f(x))+dxd(5x)+dxd(3sinx)+dxd(4cosx)
ϕ′(x)=3(f(x))2f′(x)−3(2f(x)f′(x))+4f′(x)+5+3cosx−4sinx
ϕ′(x)=3(f(x))2f′(x)−6f(x)f′(x)+4f′(x)+5+3cosx−4sinx
Factor out f′(x) from the first three terms:
ϕ′(x)=f′(x)(3(f(x))2−6f(x)+4)+5+3cosx−4sinx
Let y=f(x). Consider the quadratic expression 3y2−6y+4. We can complete the square:
3y2−6y+4=3(y2−2y)+4=3(y2−2y+1−1)+4=3((y−1)2−1)+4=3(y−1)2−3+4=3(y−1)2+1.
Since (y−1)2≥0 for all real y, 3(y−1)2≥0, so 3(y−1)2+1≥1.
Thus, 3(f(x))2−6f(x)+4≥1 for all x∈R.
Now consider the term 5+3cosx−4sinx. The expression 3cosx−4sinx can be written in the form Rcos(x+α), where R=32+(−4)2=9+16=25=5.
So, 3cosx−4sinx=5(53cosx−54sinx). Let cosα=3/5 and sinα=4/5. Then 3cosx−4sinx=5(cosαcosx−sinαsinx)=5cos(x+α).
The range of cos(x+α) is [−1,1], so the range of 5cos(x+α) is [−5,5].
The term 5+3cosx−4sinx=5+5cos(x+α). Its range is [5−5,5+5]=[0,10].
Thus, 5+3cosx−4sinx≥0 for all x∈R.
So, ϕ′(x)=f′(x)(3(f(x))2−6f(x)+4)+(5+3cosx−4sinx).
Let A(x)=3(f(x))2−6f(x)+4 and B(x)=5+3cosx−4sinx.
We have A(x)≥1 and B(x)≥0.
ϕ′(x)=f′(x)A(x)+B(x).
Let's examine the given options:
-
ϕ is increasing whenever f is increasing.
If f is increasing, then f′(x)≥0.
Since f′(x)≥0 and A(x)≥1, the term f′(x)A(x)≥0.
Since B(x)≥0, ϕ′(x)=f′(x)A(x)+B(x)≥0+0=0.
If f′(x)>0 for an interval, then f′(x)A(x)>0 (since A(x)≥1), and B(x)≥0, so ϕ′(x)>0.
If f′(x)=0 for an interval, then ϕ′(x)=B(x)≥0.
In both cases, ϕ′(x)≥0. Thus, ϕ is increasing whenever f is increasing. This option is correct. -
ϕ is increasing whenever f is decreasing.
If f is decreasing, then f′(x)≤0.
ϕ′(x)=f′(x)A(x)+B(x). Since f′(x)≤0 and A(x)≥1, f′(x)A(x)≤0.
So ϕ′(x)=(≤0)+(≥0). The sign of ϕ′(x) is not guaranteed to be positive. For example, if f′(x) is a large negative number, f′(x)A(x) will be a large negative number, which might outweigh B(x). This option is incorrect. -
ϕ is decreasing whenever f is decreasing.
If f is decreasing, then f′(x)≤0.
ϕ′(x)=f′(x)A(x)+B(x)=(≤0)+(≥0).
The sign of ϕ′(x) is not guaranteed to be negative. For example, if f′(x)=0, ϕ′(x)=B(x)≥0, so ϕ is increasing or constant. If f′(x) is slightly negative, f′(x)A(x) might be small in magnitude and negative, while B(x) can be up to 10, making ϕ′(x) positive. This option is incorrect. -
ϕ is decreasing if f′(x)=−11.
If f′(x)=−11, then ϕ′(x)=(−11)A(x)+B(x).
We know A(x)≥1 and B(x)∈[0,10].
So, −11A(x)≤−11(1)=−11.
ϕ′(x)=−11A(x)+B(x). The maximum value of B(x) is 10.
Therefore, ϕ′(x)≤−11+10=−1.
Since ϕ′(x)≤−1<0 for all x, ϕ(x) is strictly decreasing if f′(x)=−11. This option is correct.
The question asks for the correct option(s). Both option 1 and option 4 are correct.
