Solveeit Logo
Login

Question

Question: Let **p**, **q**, **r** be three mutually perpendicular vectors of the same magnitude. If vector **x...

Let p, q, r be three mutually perpendicular vectors of the same magnitude. If vector x satisfies equation p×∣(x−q)×p∣+q×∣(x−r)×q∣+r×∣(x−p)×r∣=0\mathbf { p } \times | ( \mathbf { x } - \mathbf { q } ) \times \mathbf { p } | + \mathbf { q } \times | ( \mathbf { x } - \mathbf { r } ) \times \mathbf { q } | + \mathbf { r } \times | ( \mathbf { x } - \mathbf { p } ) \times \mathbf { r } | = 0 , then x is given by

A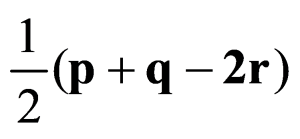
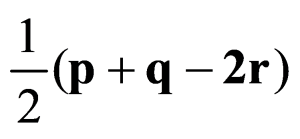
B

12(p+q+r)\frac { 1 } { 2 } ( \mathbf { p } + \mathbf { q } + \mathbf { r } )

C

13(p+q+r)\frac { 1 } { 3 } ( \mathbf { p } + \mathbf { q } + \mathbf { r } )

D

13(2p+q−r)\frac { 1 } { 3 } ( 2 \mathbf { p } + \mathbf { q } - \mathbf { r } )

Answer

12(p+q+r)\frac { 1 } { 2 } ( \mathbf { p } + \mathbf { q } + \mathbf { r } )

Explanation

Solution

Let ∣p∣=∣q∣=∣r∣=k| \mathbf { p } | = | \mathbf { q } | = | \mathbf { r } | = \mathbf { k }

∴\therefore p=kp^,q=kq^,r=kr^\mathbf { p } = k \hat { \mathbf { p } } , \mathbf { q } = k \hat { \mathbf { q } } , \mathbf { r } = k \hat { \mathbf { r } }

Let

Now, p×{x−q}×p}\mathbf { p } \times \{ \mathbf { x } - \mathbf { q } \} \times \mathbf { p } \} =

=

= = k2(x−q)k ^ { 2 } ( \mathbf { x } - \mathbf { q } ) – ∣p∣2(p^⋅x^)p^| \mathbf { p } | ^ { 2 } ( \hat { \mathbf { p } } \cdot \hat { \mathbf { x } } ) \hat { \mathbf { p } } = k2{x−q−αp^)k ^ { 2 } \{ \mathbf { x } - \mathbf { q } - \alpha \hat { \mathbf { p } } )

∴\therefore p×{(x−q)×p}+q×(x−r)×q}+r×{(x−p)×r}=0\mathbf { p } \times \{ ( \mathbf { x } - \mathbf { q } ) \times \mathbf { p } \} + \mathbf { q } \times ( \mathbf { x } - \mathbf { r } ) \times \mathbf { q } \} + \mathbf { r } \times \{ ( \mathbf { x } - \mathbf { p } ) \times \mathbf { r } \} = \mathbf { 0 }

̃ k2{x−q−αp+x−r−βq+x−p−γr}=0k ^ { 2 } \{ \mathbf { x } - \mathbf { q } - \alpha \mathbf { p } + \mathbf { x } - \mathbf { r } - \beta \mathbf { q } + \mathbf { x } - \mathbf { p } - \gamma \mathbf { r } \} = 0

̃ 3x−(p+q+r)−(αp+βq+γr)=03 \mathbf { x } - ( \mathbf { p } + \mathbf { q } + \mathbf { r } ) - ( \alpha \mathbf { p } + \beta \mathbf { q } + \gamma \mathbf { r } ) = 0

̃ 3x−(p+q+r)−x=03 \mathbf { x } - ( \mathbf { p } + \mathbf { q } + \mathbf { r } ) - \mathbf { x } = 0

̃ 2x−(p+q+r)=02 \mathbf { x } - ( \mathbf { p } + \mathbf { q } + \mathbf { r } ) = 0 ∴\therefore