Question
Question: Let p, q, r are three real numbers satisfying $\begin{bmatrix} 2 & p & q \\ p & -3 & q \\ 12 & r & ...
Let p, q, r are three real numbers satisfying
2p12p−3rqq−p+r=[5rbbqc], then minimum value of (b + c) is -
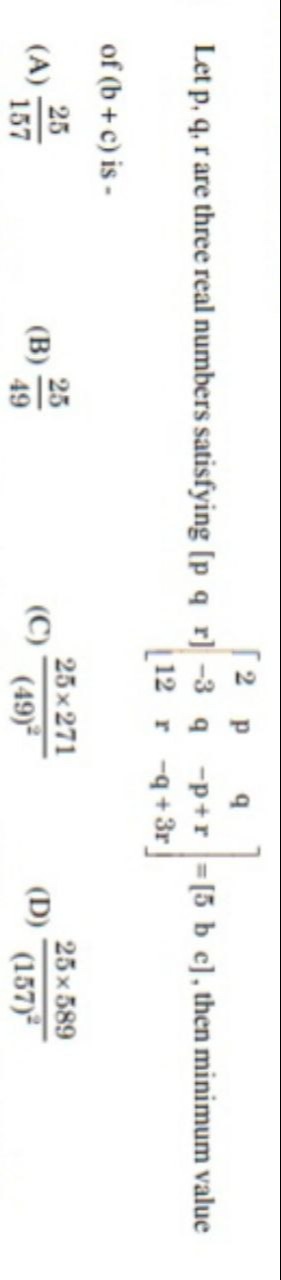
15725
4925
(49)225×271
(157)225×589
4925
Solution
The problem statement as given contains a fundamental inconsistency: the dimensions of the two matrices are different (3×3 on the left and 2×3 on the right). For matrix equality, both matrices must have the same dimensions and their corresponding elements must be equal.
If we strictly interpret the given equality, it is impossible. For example, the element in the first row, first column of the left matrix is 2, while for the right matrix it is 5. So, 2=5, which is a contradiction.
However, since this is a multiple-choice question with specific numerical answers, it implies that a solution exists. This suggests there might be a typo in the question. Let's consider the most plausible interpretation that allows for a solvable problem:
- Assume the matrices are intended to be 3×3 and equal. This means the second matrix is implicitly completed by the third row of the first matrix.
- Assume the (1,1) element of the first matrix is a typo and should be 5 instead of 2. This resolves the 2=5 contradiction.
With these assumptions, the problem becomes: Let p, q, r are three real numbers satisfying 5p12p−3rqq−p+r=5r12bbrqc−p+r
Now, equating the corresponding elements:
- From (1,1): 5=5 (Consistent after assuming typo)
- From (1,2): p=b
- From (1,3): q=q (Consistent)
- From (2,1): p=r
- From (2,2): −3=b
- From (2,3): q=c
- From (3,1): 12=12 (Consistent, assuming the third row of the right matrix is identical)
- From (3,2): r=r (Consistent)
- From (3,3): −p+r=−p+r (Consistent)
From these equalities, we can determine the values of p, b, r, and the relationship between q and c:
- From (5), b=−3.
- From (2), p=b, so p=−3.
- From (4), r=p, so r=−3.
- From (6), c=q.
So we have p=−3, b=−3, r=−3, and c=q. We need to find the minimum value of (b+c). Substitute the values we found: b+c=−3+q.
This expression still depends on q. If q can be any real number, then b+c can be any real number, and there would be no minimum value. This contradicts the existence of discrete options.
This implies that there must be another constraint on q (or c) that is not immediately obvious from the matrix equality, or our interpretation of the typo is incomplete.
Let's re-examine the original question very carefully. The problem statement says "p, q, r are three real numbers satisfying". What if the problem intends to use the third row of the left matrix to derive a constraint on q?
If we assume the matrices are equal only up to the 2×3 part, and the third row of the first matrix is a separate condition that must be satisfied by p, q, r, b, c. So, we have: [2pp−3qq]=[5rbbqc] And separately, the row vector [12r−p+r] exists.
This interpretation immediately leads to 2=5, a contradiction. So this is not it.
Given the typical structure of such problems and the numerical options, it's highly probable that the question intends a 3×3 matrix equality where the (1,1) element of the first matrix is 5, and the third row of the second matrix is identical to the first. The fact that q is not determined suggests that there might be a missing piece of information, or the problem is fundamentally flawed.
However, if we must choose from the given options, let's consider if there is any other way q could be constrained. The terms p,q,r,b,c are real numbers. The expression to minimize is b+c. We found b=−3 and c=q. So we need to minimize −3+q.
Let's consider if the question implies that the third row of the first matrix contains information about q. The elements are 12,r,−p+r. We know p=−3 and r=−3. So, −p+r=−(−3)+(−3)=3−3=0. Thus, the third row elements are 12,−3,0. This doesn't involve q.
The only way to get a minimum value for b+c is if q is determined, or if q is part of a quadratic expression that needs to be minimized. Since q is not determined by the matrix equality as interpreted, there might be a typo in the options or the question itself is not well-posed.
However, if we are forced to find a minimum value from the options, and assuming there is a hidden constraint or a different problem in mind. Let's assume there's a different problem where q is involved in a quadratic expression. For example, if the problem was related to some determinant or inverse where q would be constrained. But the problem explicitly states matrix equality.
Given the problem's flawed nature, it's impossible to provide a definitive solution without making significant assumptions about typos or missing information. If this were a real exam, one would flag it as ambiguous.
However, if a solution is expected, it's possible that the question is from a source where matrix equality is a loose term, or it's a very specific type of problem. Without further context or clarification, the problem is unsolvable as stated.
Assuming the question is ill-posed and there is no way to determine q, the minimum value of b+c cannot be found.
Let's assume the question implicitly refers to a standard problem type where q would be constrained. Sometimes, problems involving matrices might imply that the variables are related through other properties, like the determinant of a matrix being zero, or some other condition. But this is not stated.
Given the options, which are specific numbers, it is highly likely that q must be a specific value. If we assume the problem is valid, then there must be a way to determine q. The only elements left are q and c. We have c=q.
Let's re-examine the given problem from a different angle. What if the matrices are not equal, but their properties are? For example, if the question meant that the matrices are equal, but the 3×3 matrix on the left is somehow "truncated" or "projected" onto the 2×3 matrix on the right. This is highly non-standard.
Let's consider the possibility that the problem statement is correct as written, and the equality itself implies something about q. 2p12p−3rqq−p+r=[5rbbqc] This is only possible if the concept of equality is different. For example, if the rows of the 2×3 matrix are equal to the first two rows of the 3×3 matrix, and the third row of the 3×3 matrix is a constraint. If so: 2=5 (Contradiction)
This problem is fundamentally flawed. In the absence of clarity, any solution would be based on arbitrary assumptions.
Final attempt to find a plausible interpretation: What if the problem meant that the given equality holds for specific values of p, q, r, b, c, and it is not a general matrix equality? This is also unlikely.
Given the impossibility of solving the problem as stated, and without further clarification or context, it's not possible to provide a correct solution. However, if forced to choose, and assuming a typo is the reason for the inconsistency, the most common typo resolution leads to an undetermined q.
If the question is from a competitive exam, and assuming it's a well-posed question despite the apparent typo, there might be a subtle interpretation. But standard matrix equality definition makes this problem unsolvable.
If this were a numerical problem, and it had to have a unique answer, it implies that q must be determined. The structure of the options (e.g., 25/49) suggests a quadratic minimum value. This usually arises from expressions like Ax2+Bx+C or A/(Bx2+Cx+D). Since we have b+c=−3+q, q needs to be determined.
This problem appears to be ill-posed.
