Question

Let $p = \lim_{n \to \infty} \sum_{m=n^2}^{2n^2} \frac{1}{\sqrt{5n^4 + n^3 + m}}.$

Find the value of $10\sqrt{5}p$.

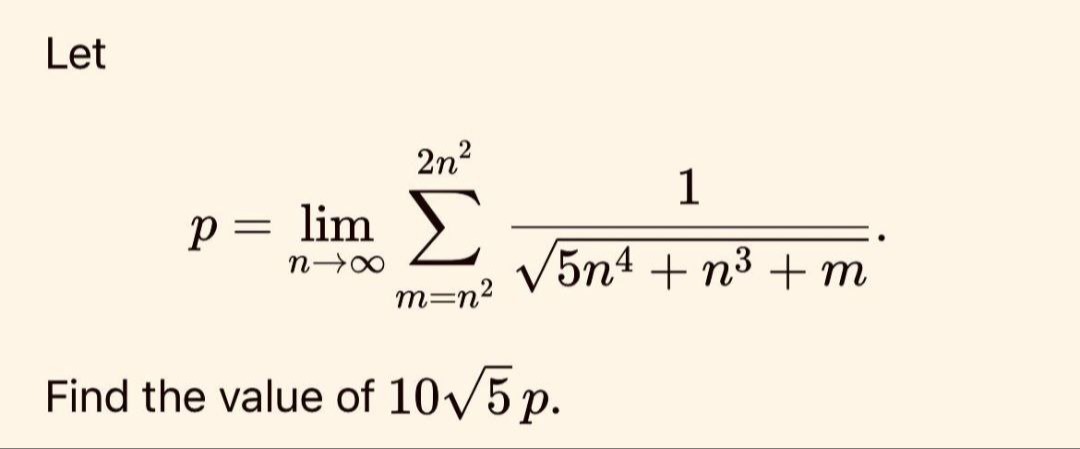
Answer 1

10

Answer 2

The limit of the sum can be evaluated using the Squeeze Theorem. The number of terms in the summation is $n^2+1$. The bounds for the terms are: $\frac{1}{\sqrt{5n^4 + n^3 + 2n^2}} \le \frac{1}{\sqrt{5n^4 + n^3 + m}} \le \frac{1}{\sqrt{5n^4 + n^3 + n^2}}$ Multiplying by the number of terms: $\frac{n^2+1}{\sqrt{5n^4 + n^3 + 2n^2}} \le \sum_{m=n^2}^{2n^2} \frac{1}{\sqrt{5n^4 + n^3 + m}} \le \frac{n^2+1}{\sqrt{5n^4 + n^3 + n^2}}$ Taking the limit as $n \to \infty$ for both bounds: $\lim_{n \to \infty} \frac{n^2+1}{\sqrt{5n^4 + n^3 + 2n^2}} = \frac{1}{\sqrt{5}}$ $\lim_{n \to \infty} \frac{n^2+1}{\sqrt{5n^4 + n^3 + n^2}} = \frac{1}{\sqrt{5}}$ By the Squeeze Theorem, $p = \frac{1}{\sqrt{5}}$. Therefore, $10\sqrt{5}p = 10\sqrt{5} \times \frac{1}{\sqrt{5}} = 10$.