Question

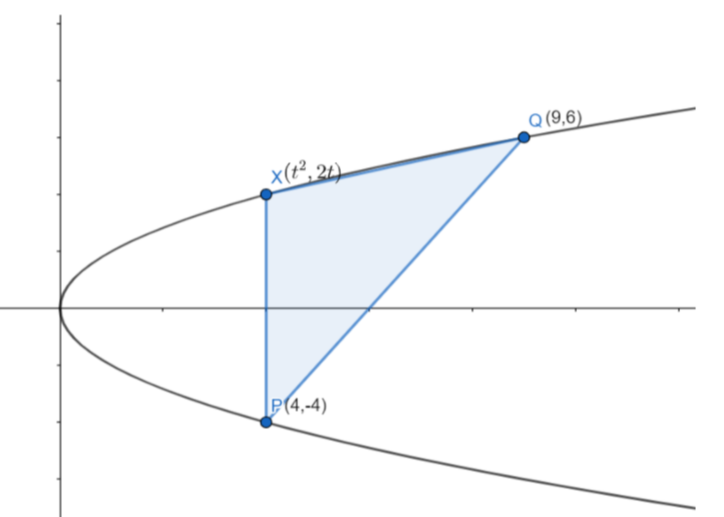
Let $P\left( 4,-4 \right)$ and $Q\left( 9,6 \right)$ be two points on a parabola ${{y}^{2}}=4x$ and X be a point on the arc POQ of this parabola, where O is the vertex of this parabola, such that the area of $\Delta PXQ$ is maximum. Then this maximum area is:

& A)\dfrac{125}{4} \\\ & B)\dfrac{125}{2} \\\ & C)\dfrac{625}{4} \\\ & D)\dfrac{75}{2} \\\ \end{aligned}$$

Answer 1

We know that a general point on the parabola ${{y}^{2}}=4ax$ is $X\left( a{{t}^{2}},2at \right)$. We know that the area of triangle whose vertices are $P\left( {{x}_{1}},{{y}_{1}} \right)$ , $Q\left( {{x}_{2}},{{y}_{2}} \right)$ and $R\left( {{x}_{3}},{{y}_{3}} \right)$, then the area of triangle $\Delta PXQ$ is equal to $\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\\ {{x}_{2}} & {{y}_{2}} & 1 \\\ {{x}_{3}} & {{y}_{3}} & 1 \\\ \end{matrix} \right|$. We know that the value of $\left| \begin{matrix} a & b & c \\\ d & e & f \\\ g & h & i \\\ \end{matrix} \right|=a\left( ei-hf \right)-b\left( di-fg \right)+c\left( dh-ge \right)$. By using these concepts, we can find the value of maximum area.

Complete step-by-step solution:
From the question, it was given that $P\left( 4,-4 \right)$ and $Q\left( 9,6 \right)$ be two points on a parabola ${{y}^{2}}=4x$ and X be a point on the arc POQ of this parabola, where O is the vertex of this parabola.
Now let us compare ${{y}^{2}}=4x$ with ${{y}^{2}}=4ax$. It is clear that the value of a is equal to 1.
We know that a general point on the parabola ${{y}^{2}}=4ax$is $X\left( a{{t}^{2}},2at \right)$.
Now we should find a general point X on the parabola ${{y}^{2}}=4x$.
So, it is clear that a general point on the parabola ${{y}^{2}}=4ax$ is $X\left( {{t}^{2}},2t \right)$.
Now we should find the area of triangle $\Delta PXQ$ whose vertices are $P\left( 4,-4 \right)$ , $Q\left( 9,6 \right)$ and $X\left( {{t}^{2}},2t \right)$.

We know that the area of triangle whose vertices are $P\left( {{x}_{1}},{{y}_{1}} \right)$ , $Q\left( {{x}_{2}},{{y}_{2}} \right)$ and $R\left( {{x}_{3}},{{y}_{3}} \right)$, then the area of triangle $\Delta PXQ$ is equal to $\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\\ {{x}_{2}} & {{y}_{2}} & 1 \\\ {{x}_{3}} & {{y}_{3}} & 1 \\\ \end{matrix} \right|$.
By using this formula, we should find the area of triangle $\Delta PXQ$ whose vertices are $P\left( 4,-4 \right)$ , $Q\left( 9,6 \right)$and $X\left( {{t}^{2}},2t \right)$.
Let us assume this area is equal to A.

4 & -4 & 1 \\\ 9 & 6 & 1 \\\ {{t}^{2}} & 2t & 1 \\\ \end{matrix} \right|$$ We know that the value of $$\left| \begin{matrix} a & b & c \\\ d & e & f \\\ g & h & i \\\ \end{matrix} \right|=a\left( ei-hf \right)-b\left( di-fg \right)+c\left( dh-ge \right)$$. $$\begin{aligned} & \Rightarrow A=\left( \dfrac{4\left( (6)(1)-(1)(2t) \right)-(-4)\left( (9)(1)-(1)({{t}^{2}}) \right)+1\left( (9)(2t)-(6)({{t}^{2}}) \right)}{2} \right) \\\ & \Rightarrow A=\left( \dfrac{4\left( 6-2t \right)+4\left( 9-{{t}^{2}} \right)+\left( 18t-6{{t}^{2}} \right)}{2} \right) \\\ & \Rightarrow A=\left( \dfrac{24-8t+36-4{{t}^{2}}+18t-6{{t}^{2}}}{2} \right) \\\ & \Rightarrow A=\left( \dfrac{-10{{t}^{2}}+10t+60}{2} \right) \\\ & \Rightarrow A=-5{{t}^{2}}+5t+30 \\\ \end{aligned}$$ Now we should find the maximum value of A. Now let us compare A with $$a{{x}^{2}}+bx+c$$. Then we get the value of a is equal to -5, the value of b is equal to 5 and the value of c is equal to 30. We know that the maximum value of $$a{{x}^{2}}+bx+c$$(if $$a<0$$) is equal to $$\dfrac{4ac-{{b}^{2}}}{4a}$$ at $$x=\dfrac{-b}{2a}$$. Now by substituting the values if a, b and c we can find the maximum value of A. Let us assume the maximum value of A is equal to $${{A}_{\max }}$$. $$\begin{aligned} & \Rightarrow {{A}_{\max }}=\dfrac{4\left( -5 \right)\left( 30 \right)-{{\left( 5 \right)}^{2}}}{4\left( -10 \right)} \\\ & \Rightarrow {{A}_{\max }}=\dfrac{-600-25}{-20} \\\ & \Rightarrow {{A}_{\max }}=\dfrac{625}{20} \\\ & \Rightarrow {{A}_{\max }}=\dfrac{125}{4} \\\ \end{aligned}$$ So, it is clear that maximum area of $$\Delta PXQ$$ is equal to $$\dfrac{125}{4}$$. **Hence, option A is correct.** **Note:** Students may have a misconception that the value of $$\left| \begin{matrix} a & b & c \\\ d & e & f \\\ g & h & i \\\ \end{matrix} \right|=a\left( ei-hf \right)+b\left( di-fg \right)+c\left( dh-ge \right)$$. If this misconception is followed, then we cannot get the correct value of maximum area of $$\Delta PXQ$$. So, this misconception should be avoided. So, students should have a clear view of this concept.