Question

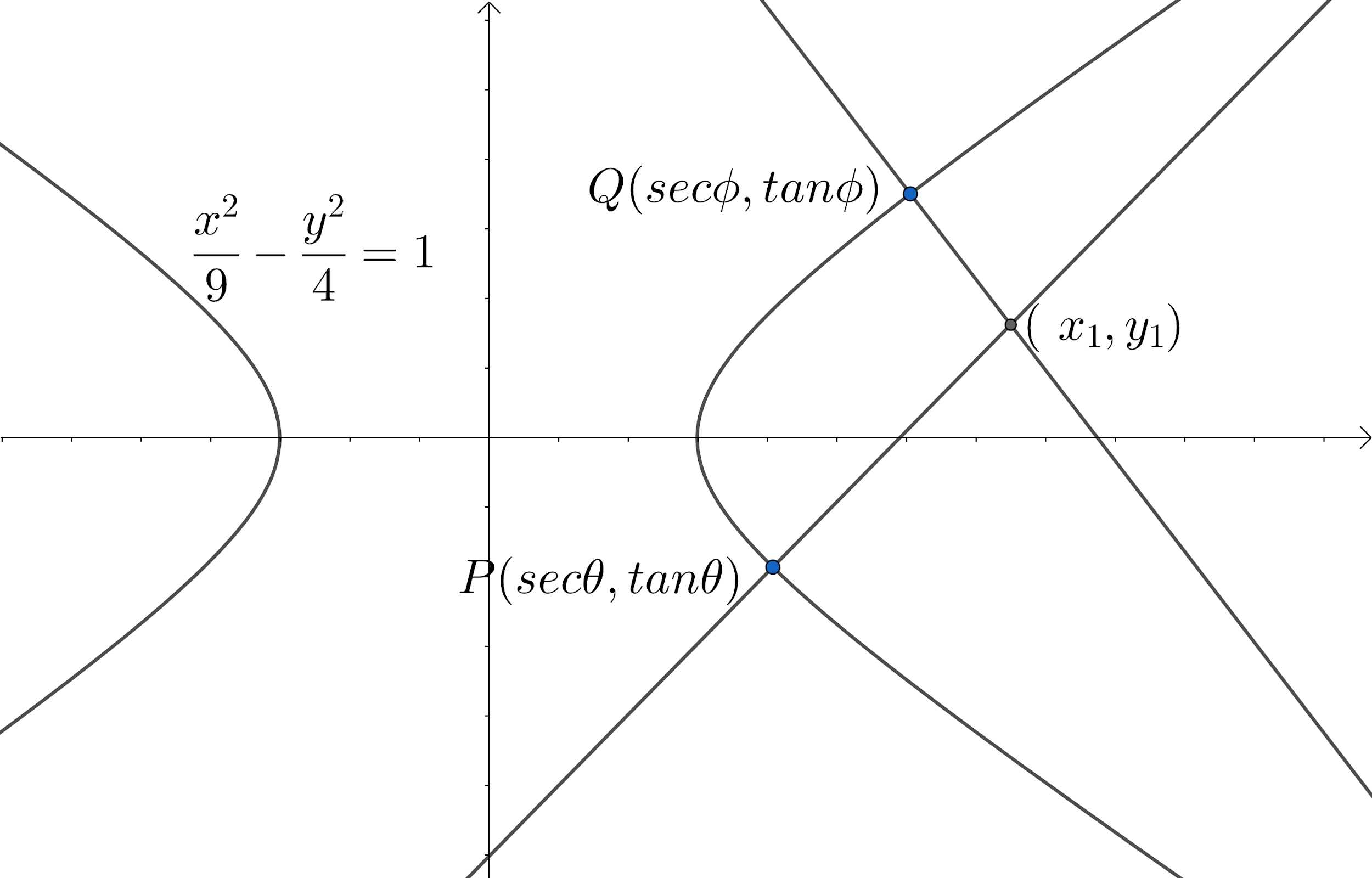
Let $P\left( 3\sec \theta ,2\tan \theta \right)$ and $Q\left( 3\sec \phi ,2\tan \phi \right)$ where $\theta +\phi =\dfrac{\pi }{2}$ , be two distinct points on the hyperbola $\dfrac{{{x}^{2}}}{9}-\dfrac{{{y}^{2}}}{4}=1$ . Then the ordinate of the point of intersection of the normals at P and Q is :-
A. $\dfrac{11}{3}$,
B. $-\dfrac{11}{3}$,
C. $-\dfrac{13}{2}$,
D. $\dfrac{13}{2}$.

Answer 1

For a hyperbola, $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. The equation of the normal at the point $A\left( {{x}_{1}},{{y}_{1}} \right)$ on it is $\dfrac{{{a}^{2}}x}{{{x}_{1}}}+\dfrac{{{b}^{2}}y}{{{y}_{1}}}={{a}^{2}}+{{b}^{2}}$. We need to write the equation of normal at P as well as at Q on the given hyperbola. Then, we have to solve these two equations simultaneously to get the point of intersection.

Complete step by step answer:
Standard equation of a hyperbola is –
$\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$……………………. (1)
We have given the equation of hyperbola is –
$\dfrac{{{x}^{2}}}{9}-\dfrac{{{y}^{2}}}{4}=1$…………………………. (2)

Comparing, the given equation of hyperbola with the standard equation of hyperbola:-
On comparing the coefficients of ${{x}^{2}}$ and ${{y}^{2}}$ in both equations (1) and (2), we get
${{a}^{2}}=9$.
Taking positive square root,
$a=3$.
And, ${{b}^{2}}=4$.
Taking positive square root,
$b=2$.
Now, the equation of normal at point P is –
Putting, ${{x}_{1}}=3\sec \theta$, ${{y}_{1}}=2\tan \theta$(in the equation of normal provided in the hint.)
We get,
$\dfrac{{{a}^{2}}x}{3\sec \theta }+\dfrac{{{b}^{2}}y}{2\tan \theta }={{a}^{2}}+{{b}^{2}}$.
Putting $a=3$and $b=2$ in the above equation
$\Rightarrow \dfrac{9x}{3\sec \theta }+\dfrac{4y}{2\tan \theta }=13$.
Since, $\cos \theta =\dfrac{1}{\sec \theta }$.
And $\cot \theta =\dfrac{1}{\tan \theta }$ .
The above equation can be written as –
$\Rightarrow 3x\left( \dfrac{1}{\sec \theta } \right)+2y\left( \dfrac{1}{\tan \theta } \right)=13$.
$\Rightarrow 3x\left( \cos \theta \right)+2y\left( \cot \theta \right)=13$.
$\Rightarrow 3\cos \theta .x+2\cot \theta .y=13$…………………… (3)
The equation of normal at point Q is –
Putting, ${{x}_{1}}=3\sec \phi$, ${{y}_{1}}=2\tan \phi$ (in the equation of normal provided in the hint.)
We get,
$\dfrac{{{a}^{2}}x}{3\sec \phi }+\dfrac{{{b}^{2}}y}{2\tan \phi }=1$.
Putting $a=3$and $b=2$ in the above equation
$\Rightarrow \dfrac{9x}{3\sec \phi }+\dfrac{4y}{2\tan \phi }=1$.
$\Rightarrow 3x\left( \dfrac{1}{\sec \phi } \right)+2y\left( \dfrac{1}{\tan \phi } \right)=1$.
We know that, $\dfrac{1}{\sec \phi }=\cos \phi$.
And $\dfrac{1}{\tan \phi }=\cot \phi$.
The above equation can be written as –
$\Rightarrow 3x\left( \cos \phi \right)+2y\left( \cot \phi \right)=1$.
$\Rightarrow 3\cos \phi .x+2\cot \phi .y=1$
Now, it is given in the equation, $\theta +\phi =\dfrac{\pi }{2}$
$\therefore \phi =\dfrac{\pi }{2}-\theta$.
Now, replacing $\phi$ by $\dfrac{\pi }{2}-\theta$ , we get –
$\Rightarrow 3\cos \left( \dfrac{\pi }{2}-\theta \right)x+2\cot \left( \dfrac{\pi }{2}-\theta \right)y=13$.
$\Rightarrow 3\left( \sin \theta \right)x+2\left( \tan \theta \right)y=13$.
$\Rightarrow 3\sin \theta .x+2\tan \theta .y=13$…………………. (4)
Now, we have to solve equation (3) and (4) simultaneously to get the value of ordinate (i.e. y coordinate) from equation (3), we can write
$\Rightarrow 3\cos \theta .x=13-2\cot \theta .y$.
$\Rightarrow x=\dfrac{13-12\cot \theta y}{3\cos \theta }$………………. (5)
From equation (4) we can write
$\Rightarrow 3\sin \theta x=13-2\tan \theta y$.
$\Rightarrow x=\dfrac{13-2\tan \theta y}{3\sin \theta }$…………………………. (6)
Equation (5) and (6) –
$\Rightarrow \dfrac{13-2y\tan \theta }{3\sin \theta }=\dfrac{13-2y\cot \theta }{3\sin \theta }$.
$\Rightarrow 13-2y\tan \theta =13\tan \theta -2y$.
$\Rightarrow 2y-2y\tan \theta =13\tan \theta -13$.
$\Rightarrow 2y\left( 1-\tan \theta \right)=13\left( \tan \theta -1 \right)$.
$\Rightarrow 2y=-13$.
$\Rightarrow y=-\dfrac{13}{2}$.
Hence, the ordinate (y-coordinate) is equal to $-\dfrac{13}{2}$.

Note:
In this question, the equation of normal in point form on the hyperbola is used. Students can make mistakes by taking ${{a}^{2}}$ as 4 and ${{b}^{2}}$ as 9 here. Be careful, while taking values of ${{a}^{2}}$ and ${{b}^{2}}$. Note that the $~\left( {{a}^{2}} \right)$ always goes with the positive of ${{x}^{2}}$ or ${{y}^{2}}$ .
In the given equation, $\dfrac{+{{x}^{2}}}{9}-\dfrac{{{y}^{2}}}{4}=1$.
Here, ${{x}^{2}}$is with a positive sign, hence it will give ${{a}^{2}}$ as 9.