Question

Let P be the point on parabola, ${{y}^{2}}=8x$ which is at a minimum distance from the center C of the circle, ${{x}^{2}}+{{\left( y+6 \right)}^{2}}=1$. Then the equation of the circle, passing through C and having its center at P is:
(a) ${{x}^{2}}+{{y}^{2}}-4x+9y+18=0$
(b) ${{x}^{2}}+{{y}^{2}}-4x+8y+12=0$
(c) ${{x}^{2}}+{{y}^{2}}-x+4y-12=0$
(d) ${{x}^{2}}+{{y}^{2}}-\dfrac{x}{4}+2y-24=0$

Answer 1

Hint: Suppose a parametric coordinate on the given parabola. Parametric coordination on ${{y}^{2}}=4ax\to \left( a{{t}^{2}},2at \right)$. Standard equation of a circle is ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$, where, $\left( {{x}_{1}}{{y}_{1}} \right)$is centre and r is the radius. Use the distance formula, for calculating distance between points $\left( {{x}_{1}}{{y}_{1}} \right),\left( {{x}_{2}}{{y}_{2}} \right)$distance formula is given as
$\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
For getting the minimum value of any function, find differentiation of it and put it to 0.

Complete step-by-step answer:
As we know coordinates in parametric form of parabola ${{y}^{2}}=4ax\to \left( a{{t}^{2}},2at \right)$, where it is a parameter.
So, we can suppose point P in parabola ${{y}^{2}}=8x\to P\left( 2{{t}^{2}},4t \right)$, where value of ‘a’ will be ‘2’ $\left( 4a=8 \right)$.
As, equation of circle given in the problem is
${{x}^{2}}+{{\left( y+6 \right)}^{2}}=1$ ……………. (i)
So, on comparing the given equation of circle with the standard equation of circle, we can get the centre of the given circle and radius as well. Standard form of a circle is given as
${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$ ……………….. (ii)
Where, $\left( {{x}_{1}}{{y}_{1}} \right)$is centre and ‘r’ is the radius.
So, we can write the equation of given circle in problem as
${{\left( x-0 \right)}^{2}}+{{\left( y-\left( -6 \right) \right)}^{2}}={{\left( 1 \right)}^{2}}$

Hence,
Centre = (0, -6)
Radius = 1.
So, we can draw diagram as

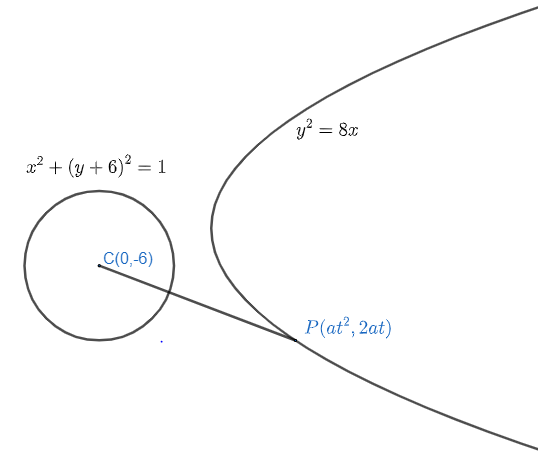
Where a = 2
As, we need to find point P on ${{y}^{2}}=8x$ which is at the minimum distance from the centre of the circle.
So, we can calculate the distance PC with the help of distance formula.
We know distance between $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ can be given by distance formula as
$AB=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$ …………….. (iii)
So, distance, PC can be calculated as
$\begin{aligned} & PC=\sqrt{{{\left( a{{t}^{2}}-0 \right)}^{2}}+{{\left( 2at-\left( -6 \right) \right)}^{2}}} \\\ & PC=\sqrt{{{a}^{2}}{{t}^{4}}+{{\left( 2at+6 \right)}^{2}}} \\\ \end{aligned}$
Squaring both sides, we get
${{\left( PC \right)}^{2}}={{a}^{2}}{{t}^{4}}+{{\left( 2at+6 \right)}^{2}}$ ……………….. (iv)
Now, we need to find the point P, which is at minimum distance from the centre. So, we need to minimize the length PC in the equation (iv). Hence, we need to differentiate the equation (iv) with respect to ‘t’ as the value of ‘a’ is ‘2’ i.e. a is constant.
So, let us suppose value of R.H.S of equation (iv) is Z. so, we get
$Z={{a}^{2}}{{t}^{4}}+{{\left( 2at+6 \right)}^{2}}$
So, differentiating with respect to ‘t’
We get
$\begin{aligned} & \dfrac{dz}{dt}=\dfrac{d}{dt}\left[ {{a}^{2}}{{t}^{4}}+{{\left( 2at+6 \right)}^{2}} \right], \\\ & \dfrac{dz}{dt}={{a}^{2}}\dfrac{d}{dt}{{t}^{4}}+\dfrac{d}{dt}{{\left( 2at+6 \right)}^{2}} \\\ \end{aligned}$
We know, $\dfrac{d}{dx}{{x}^{n}}=n{{x}^{n-1}}$
So, we get
$\begin{aligned} & \dfrac{dz}{dt}={{a}^{2}}\left( 4{{t}^{3}} \right)+2\left( 2at+6 \right)\left( 2a \right) \\\ & =4{{a}^{2}}{{t}^{3}}+4a\left( 2at+6 \right) \\\ & \dfrac{dz}{dt}=4a\left( a{{t}^{3}}+2at+6 \right) \\\ \end{aligned}$
Now, to get the minimum value of z, $\dfrac{dz}{dt}$ should be equal to 0. So, we get
$4a\left( a{{t}^{3}}+2at+6 \right)=0$
Put a = 2, we get
$\begin{aligned} & 8\left( 2{{t}^{3}}+4t+6 \right)=0 \\\ & 16\left( {{t}^{3}}+2t+3 \right)=0 \\\ \end{aligned}$
${{t}^{3}}+2t+3=0$…………………. (v)
Now, we need to factorize the above expression to get the value of ‘t’.
So, by observation or hit and trial method, put t = -1 to the equation v).
So, we get
-1 – 2 + 3 = 0
Hence, t = -1 is the root of equation of (v)
So, (t + 1) will be a factor of it. So, we can divide ${{t}^{3}}+2t+3\to \left( t+1 \right)$ to get other factors. So, we can write ${{t}^{3}}+2t+3$ as:
$\begin{aligned} & {{t}^{3}}+2t+3={{t}^{2}}\left( t+1 \right)-t\left( t+1 \right)+3\left( t+1 \right) \\\ & \left( {{t}^{2}}+2t+3 \right)=\left( {{t}^{2}}-t+3 \right)\left( t+1 \right) \\\ \end{aligned}$
Now, equating them to 0 from equation (v). we get
$\begin{aligned} & \left( t+1 \right)\left( {{t}^{2}}-t+3 \right)=0 \\\ & t+1=0,{{t}^{2}}-t+3=0 \\\ & t=-1,{{t}^{2}}-t+3=0 \\\ \end{aligned}$
Now, check the discrimination of quadratic
${{t}^{2}}-t+3=0\to D={{b}^{2}}-4ac$
So, we get $D={{\left( -1 \right)}^{2}}-4\times 1\times 3$
= 1 – 12 = - 11
So, D < 0, hence, it will not have any root.
Hence, point P can be given as
$=P\left( a{{t}^{2}},2at \right)$
Put a = 2, t = -1
We get
$=\left( 2{{\left( -1 \right)}^{2}},2\times 2\times \left( -1 \right) \right)$
= P (2, -4)
Now, we need to find a circle passing through the centre of ${{x}^{{}}}+{{\left( y+6 \right)}^{2}}=1$ and having centre
(2, -4).
So, we can write the equation of the circle with centre (2, -4) from the standard form of the circle from the equation (ii). So,
We get
${{\left( x-2 \right)}^{2}}+{{\left( y+4 \right)}^{2}}={{r}^{2}}$ …………….. (vi)
Where r is the radius of the circle.
As, now equation (vi) is passing through the centre of the circle of equation (i), i.e. through (0, -6). So, now we can put (0, -6) to equation (vi). Hence, we get
$\begin{aligned} & {{\left( 0-2 \right)}^{2}}+{{\left( -6+4 \right)}^{2}}={{r}^{2}} \\\ & 4+4={{r}^{r}} \\\ & {{r}^{2}}=8 \\\ \end{aligned}$
$r=2\sqrt{2}$……………….. (vii)
Now, put the value of r from the above equation to equation (vi). So, we get
$\begin{aligned} & {{\left( x-2 \right)}^{2}}+{{\left( y+4 \right)}^{2}}={{\left( 2\sqrt{2} \right)}^{2}}=8 \\\ & {{x}^{2}}+4-4x+{{y}^{2}}+16+8y=8 \\\ & {{x}^{2}}+{{y}^{2}}-4x+8y+12=0 \\\ \end{aligned}$
Hence, option (b) is the correct option.

Note: One can suppose general point on the parabola ${{y}^{2}}=8x$ as well i.e. as $\left( {{h}_{1}}k \right)$ or any else.
But here, we need to use the relation ${{k}^{2}}=8h$ (if point supposed is $\left( {{h}_{1}}k \right)$) with the whole equation. As the number of variables will be reduced if we use parametric coordinates on any conic rather than supposing any general point and solution will get flexible as well by using parametric coordinates. Use the concept of tangent at any curve that tangent always touches any curve at only one point.
One may make the solution complex if he/she differentiate the equation of length from to point in its square root form. As we know ‘z’ will be minimum. So, minimize the square of distance between the centres.