Question

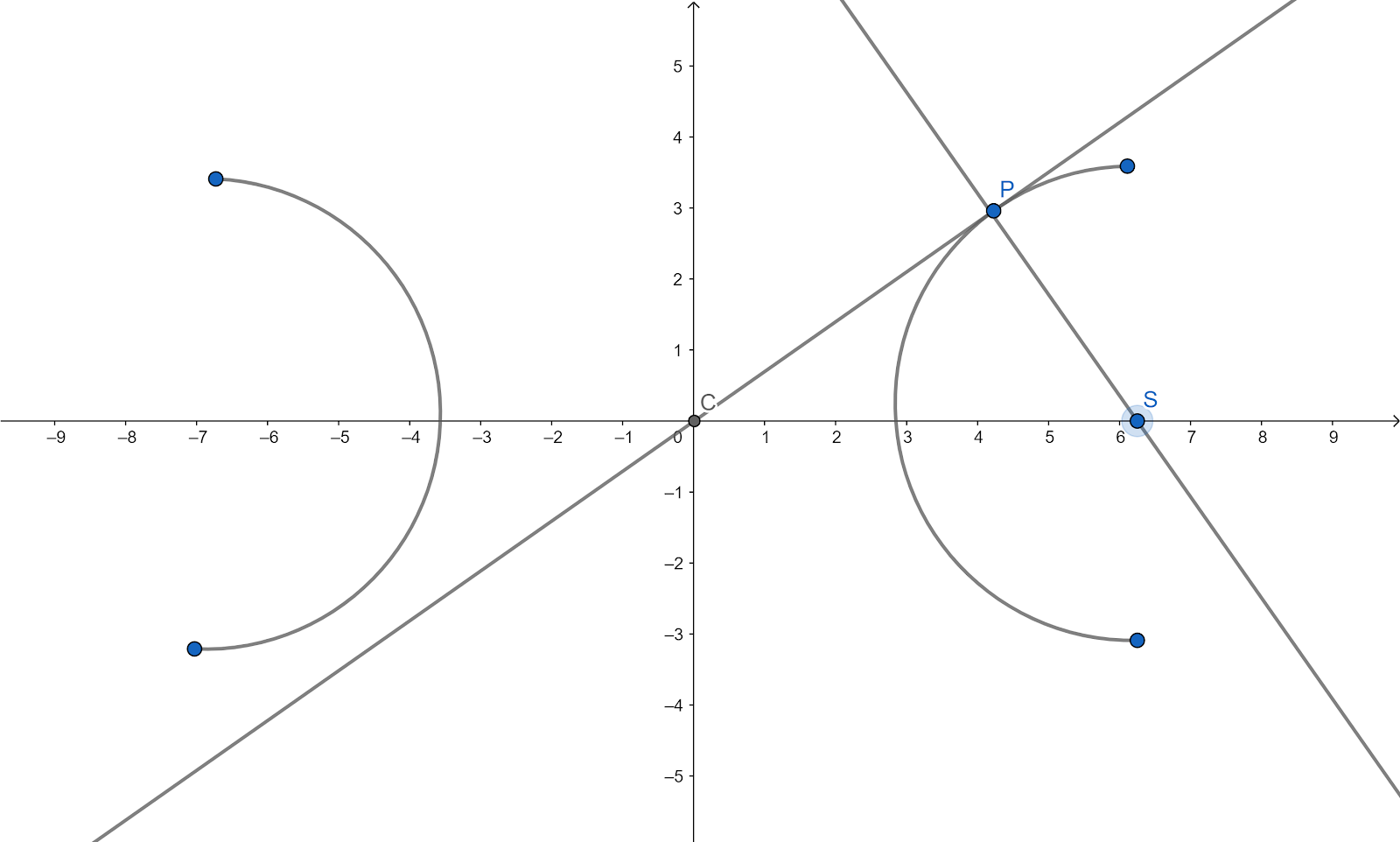
Let P be the foot of the perpendicular from focus S of hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ on the line $bx-ay=0$and let C be the centre of the hyperbola. Then the area of the rectangle whose sides are equal to that of SP and CP is
A. $2ab$
B. $ab$
C. $\dfrac{({{a}^{2}}+{{b}^{2}})}{2}$
D. $\dfrac{a}{b}$

Answer 1

Before solving this question we should be aware of the basics of hyperbola. Here in this question we are going to find the lengths of SP and CP and then find the area of the rectangle having sides equal to that of SP and CP. We will find the coordinates of P $\left( x,y \right)$ using the formula that the coordinates of P$\left( x,y \right)$ the foot of the perpendicular from S$\left( {{x}_{1}},{{y}_{1}} \right)$ on the line $ax+by=0$ is given by$\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{a{{x}_{1}}+b{{y}_{1}}}{{{a}^{2}}+{{b}^{2}}}$.

Complete step-by-step answer:
From the question we have the equation of the line CP:$bx-ay=0$. From the concept, here the coordinates of the focus S will be $\left( ae,0 \right)$ where $e$ is the eccentricity of the hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ given by: $\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{a}$ .

$\Rightarrow$ $ae=\sqrt{{{a}^{2}}+{{b}^{2}}}$

Here P is the foot of the perpendicular from S on the line$bx-ay=0$.

The distance of a point P$\left( {{x}_{1}},{{y}_{1}} \right)$ from a line $ax-by=0$ is given by the formula: $\left| \dfrac{a{{x}_{1}}-b{{y}_{1}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$.
Distance between S and P= SP = $\left| \dfrac{bae-a0}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$
$\Rightarrow$ $\left| \dfrac{bae}{ae} \right|$
$\Rightarrow |b|$.

We know that the coordinates of a point P$\left( x,y \right)$ the foot of the perpendicular from S$\left( {{x}_{1}},{{y}_{1}} \right)$ on the line $ax+by=0$ is given by $\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{a{{x}_{1}}+b{{y}_{1}}}{{{a}^{2}}+{{b}^{2}}}$
By using the above described formula. Here, the co-ordinates of P can be given by
$\dfrac{x-ae}{b}=\dfrac{y-0}{-a}=\dfrac{-(abe-0)}{{{\left( \sqrt{{{a}^{2}}+{{b}^{2}}} \right)}^{2}}}$
$\Rightarrow$ $\dfrac{x-ae}{b}=\dfrac{y}{-a}=\dfrac{-b}{ae}$
$\Rightarrow$ $y=\dfrac{ab}{ae}$ & $x=\dfrac{-{{b}^{2}}}{ae}+ae$
$\Rightarrow$ $x=\dfrac{-{{b}^{2}}+{{\left( ae \right)}^{2}}}{ae}$
$\Rightarrow$ $x=\dfrac{-{{b}^{2}}+{{a}^{2}}+{{b}^{2}}}{ae}$
$\Rightarrow$ $x=\dfrac{{{a}^{2}}}{ae}$
Hence, the coordinates of P are $\left( \dfrac{{{a}^{2}}}{ae},\dfrac{ab}{ae} \right)$
We know the coordinates of C are (0, 0) from the concept of hyperbola.
We know that the distance between the $\left( 0,0 \right)$and $\left( x,y \right)$ is given by the distance formula: $\sqrt{x{}^{2}+{{y}^{2}}}$.
Distance between C and P = CP = $\sqrt{{{\left( \dfrac{{{a}^{2}}}{ae} \right)}^{2}}+{{\left( \dfrac{ab}{ae} \right)}^{2}}}$

$\Rightarrow$ $\sqrt{\dfrac{\left( {{a}^{2}}+{{b}^{2}} \right){{a}^{2}}}{{{(ae)}^{2}}}}$

$\Rightarrow |a|$

Hence the area of the rectangle whose sides are equal to that of SP and CP is
Length of SP x length of CP

$\Rightarrow a\times b$

$\Rightarrow$ $ab$

So, the correct answer is “Option b”.

Note: We should take care while finding the coordinates of the point and distance between the points. No mistakes should be made. Here, we should make sure that we use the eccentricity formula for hyperbola correctly. The eccentricity of the hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ given by: $\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{a}$ .
$\Rightarrow$ $ae=\sqrt{{{a}^{2}}+{{b}^{2}}}$.
Similarly, if we consider eccentricity for ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ it is given by: $\sqrt{\dfrac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}}}$.
If we misconceptual use the eccentricity for ellipse instead of parabola we will completely encounter a different answer.