Question

Let $P$ be any point on a directrix of an ellipse of eccentricity $e$ . $S$ be the corresponding focus and $C$ the centre of the ellipse. The line $PC$ meets the ellipse at $A$ . The angle between $PS$ and tangent at $A$ is $\alpha$ , then $\alpha$ is equal to
a. ${\tan ^{ - 1}}e$
b. $\dfrac{\pi }{2}$
c. ${\tan ^{ - 1}}\left( {1 - {e^2}} \right)$
d.None of these

Answer 1

Hint : The point $P$ is equal to $\left( {\dfrac{a}{e},Y} \right)$ , since the point $y$ meets in ellipse so $y$ is equal to the point $x\left( {\dfrac{{\dfrac{Y}{a}}}{e}} \right)$ . Then substitute $y$ in the equation of ellipse to find the tangent at $A$ . Then we will determine slope in $PS$ . Product of the lope $PS$ and $A$ is equal to $- 1$ which will help to determine the value of $\alpha$ .

Complete step-by-step answer :
The following is the schematic diagram of the ellipse in which $S$ is the corresponding focus and $C$ is the centre of the ellipse.

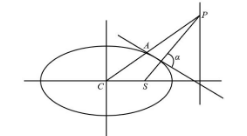
From the above diagram we observe that the point $A$ is $\left( {a\cos \theta ,b\sin \theta } \right)$ which is $\left( {{x_1},{y_1}} \right)$ . The point $S$ is in the $S\left( {ae,0} \right)$ and the point $C$ is $\left( {0,0} \right)$ .
Equation of ellipse is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ .
Now, let the point $P$ is in the outer part of ellipse,
$P\left( {\dfrac{a}{e},Y'} \right) = \left( {\dfrac{a}{e},Y} \right)$
Since we know that the point $y$ meets at ellipse at $A$ that is at $\left( {{x_1},{y_1}} \right)$ we get,
$y = x\left( {\dfrac{{\dfrac{Y}{a}}}{e}} \right)$
Now, we know that the equation of ellipse is,
$\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$
Since $y$ lies in the ellipse so the equation changes to,
$\begin{array}{c} \dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\\\ \dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{\dfrac{{{x^2}{Y^2}}}{{{a^2}{e^2}}}}}{{{b^2}}} = 1 \end{array}$
On further solving the above expression, we get the value as,
$\dfrac{{{x^2}}}{{{a^2}}} + {x^2}{Y^2}\dfrac{{\left( {{a^2} - {b^2}} \right)}}{{{b^2}}} = 1$
Since, the eccentricity $e$ is equal to $\sqrt {{a^2} - {b^2}}$ . So, let us substitute the value we obtain,
$\begin{array}{l} \dfrac{{{x^2}}}{{{a^2}}} + {x^2}{Y^2}\dfrac{{{e^2}}}{{1 - {e^2}}} = 1\\\ {x^2}\left( {\dfrac{1}{{{a^2}}} + \dfrac{{{Y^2}{e^2}}}{{1 - {e^2}}}} \right) = 1\\\ \end{array}$
The take term $\left( {\dfrac{1}{{{a^2}}} + \dfrac{{{Y^2}{e^2}}}{{1 - {e^2}}}} \right)$ to the right side and then take the square root both sides then we get,
$\begin{array}{l} {x^2} = \dfrac{1}{{\left( {\dfrac{1}{{{a^2}}} + \dfrac{{{Y^2}{e^2}}}{{1 - {e^2}}}} \right)}}\\\ x = \dfrac{1}{{\sqrt {\left( {\dfrac{1}{{{a^2}}} + \dfrac{{{Y^2}{e^2}}}{{1 - {e^2}}}} \right)} }} \end{array}$
This implies that $x = \dfrac{1}{{\sqrt {\left( {\dfrac{1}{{{a^2}}} + \dfrac{{{Y^2}{e^2}}}{{1 - {e^2}}}} \right)} }}$ .
Now, we have to find the slope of the tangent at the point $A$ is equal to $- \dfrac{{{b^2}}}{{{a^2}}}\dfrac{{{x_1}}}{{{y_1}}}$ .
Since, we know that $y = x\left( {\dfrac{{\dfrac{Y}{a}}}{e}} \right)$ , let us substitute in the above equation, so we get,
$\begin{array}{c} {T_{\rm{A}}} = - \dfrac{{{b^2}}}{{{a^2}}} \times \dfrac{{\dfrac{a}{e}}}{Y}\\\ = - \left( {1 - {e^2}} \right) \times \dfrac{a}{{eY}} \end{array}$
Also, slope of $PS$ is equal to,
$\dfrac{Y}{{\dfrac{{a{e^2}}}{{1 - {e^2}}}}} = \dfrac{{Ye}}{{a\left( {1 - {e^2}} \right)}}$
Now, we will calculate the product of slope of $PS$ and ${T_A}$ which is given as,
$\begin{array}{l} = \left[ { - \left( {1 - {e^2}} \right) \times \dfrac{a}{{eY}}} \right] \times \left[ {\dfrac{{Ye}}{{a\left( {1 - {e^2}} \right)}}} \right]\\\ = - 1 \end{array}$

Then, we can say that $\alpha = \dfrac{\pi }{2}$ because PS is perpendicular to the tangent.
Hence, the correct option is $\dfrac{\pi }{2}$ .
So, the correct answer is “Option b”.

Note : Do not forget to take the $y$ at the $x\left( {\dfrac{{\dfrac{Y}{a}}}{e}} \right)$ and this can. also be done by different methods. Also, take $A$ as $\left( {a\cos \theta ,b\sin \theta } \right)$ and equation of $AC$ is $y = \dfrac{b}{a}x\tan \theta$ where, $\tan \theta$ is the slope.