Question
Question: Let $P$ be a square matrix such that $P^2=I-P$. For $\alpha$, $\beta$, $\gamma$, $\delta \in N$, if ...
Let P be a square matrix such that P2=I−P. For α, β, γ, δ∈N, if Pα+Pβ+29P=γI and Pα=Pβ+δI−13P, then 5α+β+γ−δ is equal to
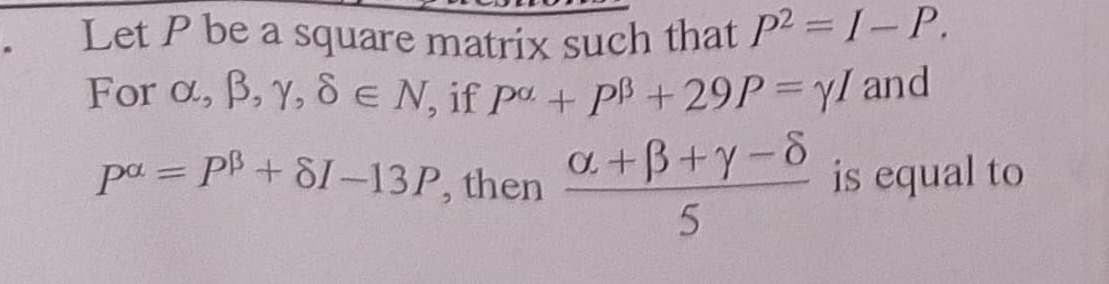
24/5
Solution
The given condition is P2=I−P. This can be rewritten as P2+P−I=0. We need to express higher powers of P in the form aP+bI.
P1=P
P2=I−P
P3=P⋅P2=P(I−P)=P−P2=P−(I−P)=2P−I
P4=P⋅P3=P(2P−I)=2P2−P=2(I−P)−P=2I−2P−P=2I−3P
P5=P⋅P4=P(2I−3P)=2P−3P2=2P−3(I−P)=2P−3I+3P=5P−3I
P6=P⋅P5=P(5P−3I)=5P2−3P=5(I−P)−3P=5I−5P−3P=5I−8P
We observe a pattern related to Fibonacci numbers Fn, where F0=0,F1=1,F2=1,F3=2,F4=3,F5=5,F6=8,F7=13,F8=21,…. The general form is Pn=(−1)n+1FnP+(−1)nFn−1I for n≥1.
We are given two equations:
- Pα+Pβ+29P=γI⟹Pα+Pβ=γI−29P
- Pα=Pβ+δI−13P⟹Pα−Pβ=δI−13P
Add equation (1) and equation (2):
(Pα+Pβ)+(Pα−Pβ)=(γI−29P)+(δI−13P)
2Pα=(γ+δ)I−42P
Subtract equation (2) from equation (1):
(Pα+Pβ)−(Pα−Pβ)=(γI−29P)−(δI−13P)
2Pβ=(γ−δ)I−16P
Now, substitute the general form for Pn into these two derived equations.
For 2Pα=(γ+δ)I−42P:
2[(−1)α+1FαP+(−1)αFα−1I]=−42P+(γ+δ)I
Comparing the coefficients of P and I:
2(−1)α+1Fα=−42⟹(−1)α+1Fα=−21
Since Fα>0 for α∈N, we must have (−1)α+1=−1, which implies α+1 is odd, so α is even.
Thus, Fα=21. From the Fibonacci sequence, F8=21, so α=8. This is consistent with α being even.
Comparing coefficients of I:
2(−1)αFα−1=γ+δ
Since α=8 (even), (−1)α=1.
2F8−1=γ+δ⟹2F7=γ+δ
2×13=γ+δ⟹γ+δ=26. (Eq. A)
For 2Pβ=(γ−δ)I−16P:
2[(−1)β+1FβP+(−1)βFβ−1I]=−16P+(γ−δ)I
Comparing the coefficients of P and I:
2(−1)β+1Fβ=−16⟹(−1)β+1Fβ=−8
Since Fβ>0 for β∈N, we must have (−1)β+1=−1, which implies β+1 is odd, so β is even.
Thus, Fβ=8. From the Fibonacci sequence, F6=8, so β=6. This is consistent with β being even.
Comparing coefficients of I:
2(−1)βFβ−1=γ−δ
Since β=6 (even), (−1)β=1.
2F6−1=γ−δ⟹2F5=γ−δ
2×5=γ−δ⟹γ−δ=10. (Eq. B)
Now we have a system of linear equations for γ and δ:
(A) γ+δ=26
(B) γ−δ=10
Adding (A) and (B):
2γ=36⟹γ=18.
Subtracting (B) from (A):
2δ=16⟹δ=8.
We have found the values:
α=8
β=6
γ=18
δ=8
All values are natural numbers, as required.
Finally, we need to calculate 5α+β+γ−δ:
58+6+18−8=514+18−8=532−8=524.
The final answer is 524.
Explanation of the solution:
- Derive the general form for Pn using the given P2=I−P relation. It is found to be Pn=(−1)n+1FnP+(−1)nFn−1I, where Fn are Fibonacci numbers (F0=0,F1=1,…).
- Manipulate the given equations Pα+Pβ+29P=γI and Pα=Pβ+δI−13P to get expressions for 2Pα and 2Pβ in the form aP+bI.
- 2Pα=−42P+(γ+δ)I
- 2Pβ=−16P+(γ−δ)I
- Equate the coefficients of P and I from the general form of Pn with the derived expressions for 2Pα and 2Pβ.
- Solve for α and β using the coefficient of P. This involves identifying the correct Fibonacci number and checking the sign to determine parity.
- Fα=21⟹α=8 (even)
- Fβ=8⟹β=6 (even)
- Solve for γ and δ using the coefficient of I.
- γ+δ=2F7=2×13=26
- γ−δ=2F5=2×5=10
- Solving these gives γ=18,δ=8.
- Substitute the values of α,β,γ,δ into the required expression 5α+β+γ−δ.
- 58+6+18−8=524.
