Question

Let $P$ be a point on the parabola ${{y}^{2}}-2y-4x+5=0$, such that the tangent on the parabola at $P$ intersects the directrix at a point $Q$. Let $R$ be the point that divides the line segment $QP$ externally in the ratio $\dfrac{1}{2}:1$. Find the locus of $R$.

Answer 1

Hint: Write the equation of tangent, get points $Q$ and $P$ and then use $x=\dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n}$ and $y=\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n}$.

We are given a point $P$ on the parabola ${{y}^{2}}-2y-4x+5=0$ such that tangent on the parabola at $P$ intersect the directrix at $Q$.
We have to find the locus of $R$ which divides $QP$ externally in the ratio $\dfrac{1}{2}:1$.
First of all, we will convert the parabola into its standard form
We take, ${{y}^{2}}-2y-4x+5=0$
Or, ${{y}^{2}}-2y=4x-5$
Adding $1$ on both sides,
We get, ${{y}^{2}}-2y+1=4x-5+1$
Since we know that ${{a}^{2}}+{{b}^{2}}-2ab={{\left( a-b \right)}^{2}}$
Therefore, we get ${{\left( y-1 \right)}^{2}}=4x-4$
Or, ${{\left( y-1 \right)}^{2}}=4\left( x-1 \right)$

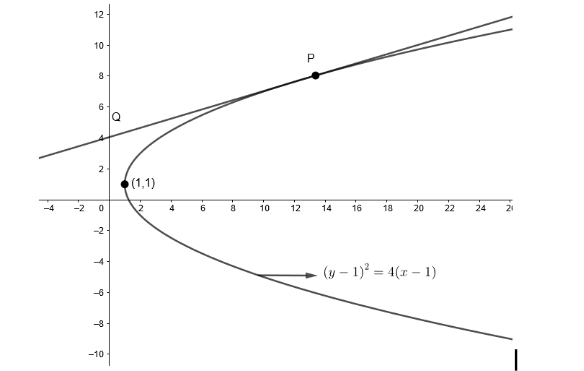
Let $y-1=Y$ and $x-1=X$
So, we get parabola ${{Y}^{2}}=4X$ which is the standard form of a parabola.
Now, we know that any general point on the parabola is $\left( a{{t}^{2}},2at \right)$.
By comparing parabola ${{Y}^{2}}=4X$ with general parabola ${{y}^{2}}=4ax$,
We get $4a=4$
Therefore, we get $a=1$
Now, we know that any general point on the parabola ${{y}^{2}}=4ax$ is $\left( a{{t}^{2}},2at \right)$
Since, $a=1$
We get, $P\left( X,Y \right)=P\left( {{t}^{2}},2t \right)$
We know that tangent at point $\left( a{{t}^{2}},2at \right)$ is given by $ty=x+a{{t}^{2}}$
Since $a=1$, we get equation of tangent at $P\left( {{t}^{2}},2t \right)$ as $tY=X+{{t}^{2}}....\left( i \right)$
We know that equation of directrix is
$X=-a$
Therefore, we get $X=-1$
Or, $X+1=0$
Since we know that $Q$ is a point of intersection of tangents and directrix is $X=-1$.
Therefore, we will put $X=-1$ in the equation $\left( i \right)$ to find the $Y$ coordinate.
So, $tY=X+{{t}^{2}}$
$\Rightarrow tY=-1+{{t}^{2}}$
$Y=\dfrac{{{t}^{2}}-1}{t}$
Therefore, we get a point $Q\left( X,Y \right)=\left( -1,\dfrac{{{t}^{2}}-1}{t} \right)$
Let the point $R$ be $\left( h,k \right)$ which divides $QP$ externally in the ratio $\dfrac{1}{2}:1$

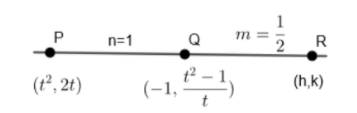
We know that if $R\left( x,y \right)$ divides $Q\left( {{x}_{1}},{{y}_{1}} \right)$ and $P\left( {{x}_{2}},{{y}_{2}} \right)$in the ratio $m:n$
Then, $x=\dfrac{m\left( {{x}_{2}} \right)-n\left( {{x}_{1}} \right)}{\left( m-n \right)}$
$y=\dfrac{m\left( {{y}_{2}} \right)-n\left( {{y}_{1}} \right)}{\left( m-n \right)}$
Here, we have $R\left( x,y \right)=\left( h,k \right)$
$Q\left( {{x}_{1}},{{y}_{1}} \right)=\left( -1,\dfrac{{{t}^{2}}-1}{t} \right)$
$P\left( {{x}_{2}},{{y}_{2}} \right)=\left( {{t}^{2}},2t \right)$
$m=\dfrac{1}{2},n=1$
So, we get $h=\dfrac{\dfrac{1}{2}\left( {{t}^{2}} \right)-1\left( -1 \right)}{\dfrac{1}{2}-1}$
$h=\dfrac{\dfrac{{{t}^{2}}}{2}+1}{\dfrac{-1}{2}}$
$h=-\left( {{t}^{2}}+2 \right)$
Or ${{t}^{2}}=-2-h....\left( ii \right)$
And $k=\dfrac{\dfrac{1}{2}\left( 2t \right)-1\left( \dfrac{{{t}^{2}}-1}{t} \right)}{\dfrac{1}{2}-1}$
$k=\dfrac{t-\left( \dfrac{{{t}^{2}}}{t}-\dfrac{1}{t} \right)}{\dfrac{-1}{2}}$
$k=-2\left[ t-\left( t-\dfrac{1}{t} \right) \right]$
$k=\dfrac{-2}{t}$
By squaring both the sides,
We get, ${{k}^{2}}=\dfrac{4}{{{t}^{2}}}$
Now, by putting the value of ${{t}^{2}}$ from equation $\left( ii \right)$
We get ${{k}^{2}}=\dfrac{4}{\left( -2-h \right)}$
By cross multiplying, we get
$\Rightarrow -{{k}^{2}}\left( h+2 \right)=4$
To get the locus, we will replace $h$by $X$ and $k$by $Y$.
We get, $-{{Y}^{2}}\left( X+2 \right)=4$
As we had assumed that $X=x-1$ and $Y=y-1$
We get, $-{{\left( y-1 \right)}^{2}}\left( x-1+2 \right)=4$
$-{{\left( y-1 \right)}^{2}}\left( x+1 \right)=4$
Or, ${{\left( y-1 \right)}^{2}}\left( x+1 \right)+4=0$

Note: Always convert the given parabola into standard parabola ${{y}^{2}}=4ax$ and then use the general equation of tangents, normals etc. Also, students often forget to convert $X$ to $x$ and $Y$ to $y$ and get wrong answers. So this step must be kept in mind.