Question

Let P and Q be the points of trisection of the line segment joining the points A (1, -2) and B (-3, 4) such that P is nearer to A. Find the coordinates of P and Q.

Answer 1

Hint: P and Q are the point of trisection, this means P and Q must be dividing the line segment AB as P is closer to A thus P will be dividing the line segment AB in the ratio 1: 2 and similar point Q will be dividing the line segment AB in ratio 2: 1. Apply this concept to the section formula to get the answer.

Complete step-by-step answer:

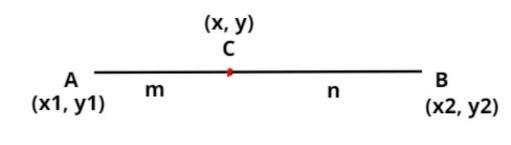
If point C divide the line AB in the ratio (m : n) internally as shown above then according to section formula the coordinates of C are:
$x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},{\text{ y}} = \dfrac{{m{y_2} + n{y_1}}}{{m + n}}$
Now it is given P and Q be the points of trisection of the line joining the points A (2, -2) and B (-7, 4) such that P is nearer to A.
Let A = (1, -2) $\equiv \left( {{x_1},{y_1}} \right)$ and B = (-3, 4) $\equiv \left( {{x_2},{y_2}} \right)$
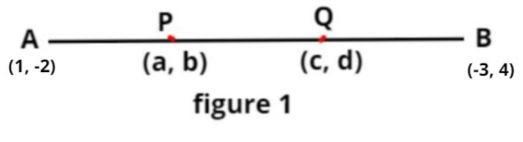
So, P and Q are points of trisection (i.e. they divide the line into three equal parts) as shown in figure 1.
So P divides the line AB in the ratio (1 : 2) internally and Q divides the line AB in the ratio (2 : 1) internally.
Let the coordinates of P be $\left( {a,b} \right)$ and the coordinates of Q be $\left( {c,d} \right)$
Therefore according to section formula the coordinates of P are,
Here the value of m = 1 and the value of n = 2.
$\Rightarrow \left( {a,b} \right) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},{\text{ }}\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right) = \left( {\dfrac{{1 \times \left( { - 3} \right) + 2 \times 1}}{{1 + 2}},\dfrac{{1 \times 4 + 2 \times \left( { - 2} \right)}}{{1 + 2}}} \right)$
Now simplify we have,
$\Rightarrow \left( {a,b} \right) = \left( {\dfrac{{ - 1}}{3},\dfrac{0}{3}} \right) = \left( { - \dfrac{1}{3},0} \right)$
Now again according to section formula the coordinates of Q are,
Here the value of m = 2 and the value of n = 1.
$\Rightarrow \left( {c,d} \right) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},{\text{ }}\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right) = \left( {\dfrac{{2 \times \left( { - 3} \right) + 1 \times 1}}{{2 + 1}},\dfrac{{2 \times 4 + 1 \times \left( { - 2} \right)}}{{2 + 1}}} \right)$
Now simplify we have,
$\Rightarrow \left( {c,d} \right) = \left( {\dfrac{{ - 5}}{3},\dfrac{6}{3}} \right) = \left( { - \dfrac{5}{3},2} \right)$
So these are the required coordinates of P and Q respectively.

Note: Whenever we face such types of questions the key concept we have to remember is that the section formula, when a point divides the line internally in the ratio (m : n) then the coordinates of that point is find according to the section formula which is stated above and the trisection of the line means that the line has three equal parts so calculate the ratio of the points P and Q which divide the line AB as above and substitute all the values in the section formula we will get the required coordinates of the points P and Q respectively.