Question

Let P and Q be the points of trisection of the line segment joining the points A (2, -2) and B (-7, 4) such that P is nearer to A. Find the coordinates of P and Q.

Answer 1

Hint: P and Q are the point of trisection, this means P and Q must be dividing the line segment AB as P is closer to A thus P will be dividing the line segment AB in the ratio 1: 2 and similar point Q will be dividing the line segment AB in ratio 2: 1. Apply this concept to the section formula to get the answer.

Complete step-by-step answer:

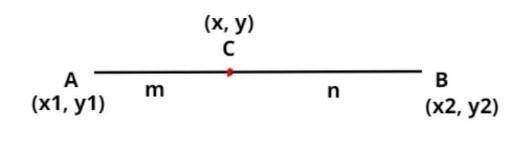
If point C divide the line AB in the ratio (m : n) internally as shown above then according to section formula the coordinates of C are:
$x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},{\text{ y}} = \dfrac{{m{y_2} + n{y_1}}}{{m + n}}$
Now it is given P and Q be the points of trisection of the line joining the points A (2, -2) and B (-7, 4) such that P is nearer to A.
Let A = (2, -2) $\equiv \left( {{x_1},{y_1}} \right)$ and B = (-7, 4) $\equiv \left( {{x_2},{y_2}} \right)$
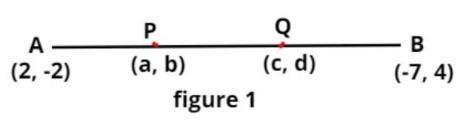
So, P and Q are points of trisection (i.e. they divide the line into three equal parts) as shown in figure 1.
So P divides the line AB in the ratio (1 : 2) internally and Q divides the line AB in the ratio (2 : 1) internally.
Let the coordinates of P be $\left( {a,b} \right)$ and the coordinates of Q be $\left( {c,d} \right)$
Therefore according to section formula the coordinates of P are,
Here the value of m = 1 and the value of n = 2.
$\Rightarrow \left( {a,b} \right) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},{\text{ }}\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right) = \left( {\dfrac{{1 \times \left( { - 7} \right) + 2 \times 2}}{{1 + 2}},\dfrac{{1 \times 4 + 2 \times \left( { - 2} \right)}}{{1 + 2}}} \right)$
Now simplify we have,
$\Rightarrow \left( {a,b} \right) = \left( {\dfrac{{ - 3}}{3},\dfrac{0}{3}} \right) = \left( { - 1,0} \right)$
Now again according to section formula the coordinates of Q are,
Here the value of m = 2 and the value of n = 1.
$\Rightarrow \left( {c,d} \right) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},{\text{ }}\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right) = \left( {\dfrac{{2 \times \left( { - 7} \right) + 1 \times 2}}{{2 + 1}},\dfrac{{2 \times 4 + 1 \times \left( { - 2} \right)}}{{2 + 1}}} \right)$
Now simplify we have,
$\Rightarrow \left( {c,d} \right) = \left( {\dfrac{{ - 12}}{3},\dfrac{6}{3}} \right) = \left( { - 4,2} \right)$
So these are the required coordinates of P and Q respectively.

Note: Whenever we face such types of problems the key concept is to have a good gist of the section formula as it is applicable to all questions in which some specific points divide a line segment into some particular ratios, this helps finding the coordinates of these specific points.