Question

Let P and Q are two square and invertible matrices, such that $\text{Q = -P}^{-1}\text{QP}$, then $(\text{P + Q})^{2}$ is equal to

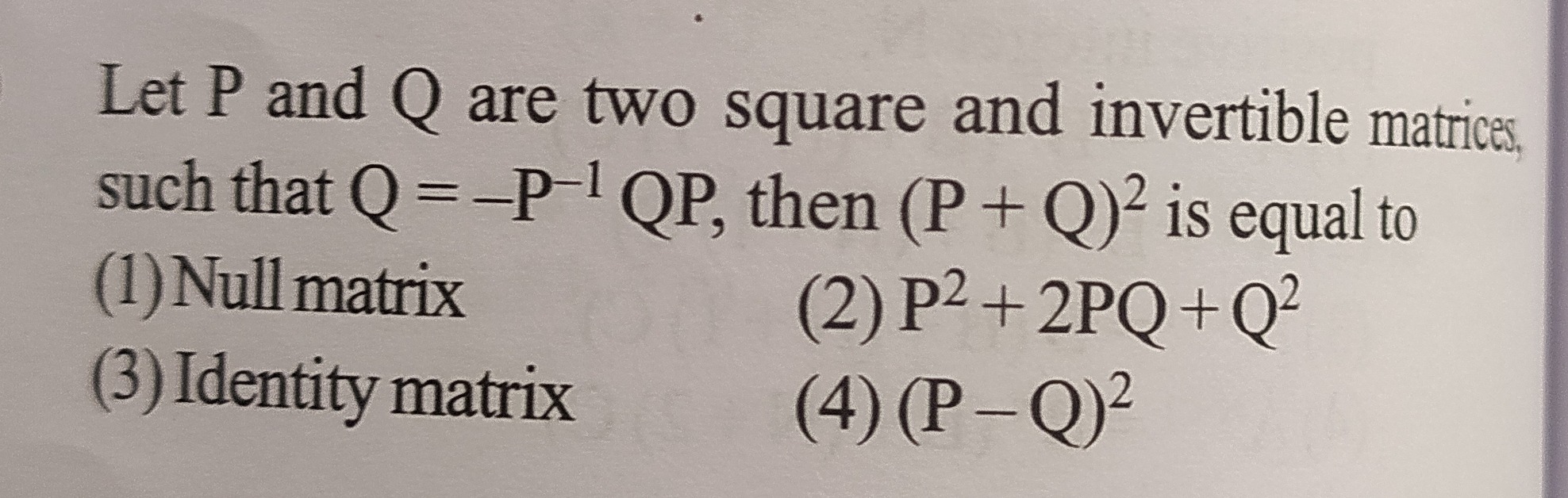
• A. Null matrix
• B. $\text{P}^{2} + 2\text{PQ}+\text{Q}^{2}$
• C. Identity matrix
• D. $(\text{P-Q})^{2}$

Answer 1

Answer: (D)

$(\text{P-Q})^{2}$

Answer 2

From the given matrix equation $\text{Q = -P}^{-1}\text{QP}$, multiply by P on the left to obtain $\text{PQ = -QP}$. This shows that P and Q are anti-commutative.

Expand $(\text{P + Q})^{2}$ as $\text{P}^2 + \text{PQ} + \text{QP} + \text{Q}^2$.

Substitute $\text{PQ = -QP}$ into the expanded form of $(\text{P + Q})^{2}$ to get $(\text{P + Q})^{2} = \text{P}^2 + (-\text{QP}) + \text{QP} + \text{Q}^2 = \text{P}^2 + \text{Q}^2$.

Expand $(\text{P-Q})^{2}$ as $\text{P}^2 - \text{PQ} - \text{QP} + \text{Q}^2$.

Substitute $\text{PQ = -QP}$ into the expanded form of $(\text{P-Q})^{2}$ to get $(\text{P-Q})^{2} = \text{P}^2 - (-\text{QP}) - \text{QP} + \text{Q}^2 = \text{P}^2 + \text{QP} - \text{QP} + \text{Q}^2 = \text{P}^2 + \text{Q}^2$.

Since both $(\text{P + Q})^{2}$ and $(\text{P-Q})^{2}$ are equal to $\text{P}^2 + \text{Q}^2$, they are equal to each other.