Question
Question: Let \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)be three unit vectors such that \(\o...
Let a,b,cbe three unit vectors such that a×(b×c)=23(b+c). If b is not parallel to c, then the angle between a and b is:
A) 43π
B) 2π
C) 32π
D) 65π
Solution
We are given that a,b,cbe three unit vectors, so, ∣a∣=∣b∣=∣c∣=1. And we know that a×(b×c)=(a.c)b−(a.b)c. This is the theorem. So on further comparing this equation, you will get the answer.
Complete step-by-step answer:
So, according to the question, we are given that a,b,cbe three unit vectors such that a×(b×c)=23(b+c).
So from this statement, it is clear that the magnitude of a,b,c are equal to 1.
∣a∣=∣b∣=∣c∣=1
Or a=b=c=1
A simple magnitude of a is written as a.
As we know that
a×(b×c)=(a.c)b−(a.b)c
And it is given that a×(b×c)=23(b+c)
Let θ be the angle between a and c.
Let β be the angle between a and b.
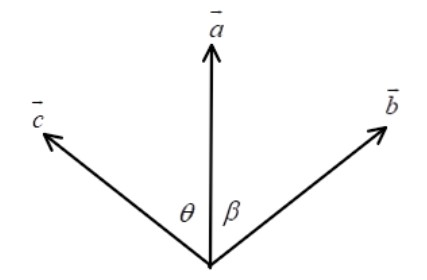
So, a.c=accosθ
Where a=c=1
So, a.c=cosθ
Similarly, a.b=abcosβ
Where a=b=1
So, a.b=cosβ
So we got that
(a.c)b−(a.b)c=23b+23c (cosθ)b−(cosβ)c=23b+23c
Upon comparing both sides, we get
cosθ=23⇒θ=30∘⇒θ=6π
And
cosβ=−23⇒β=(π−6π)⇒β=65π
So here we assume angle between a and b is β that is 65π
So, the correct answer is “Option D”.
Note: If b becomes parallel to c, then, b×c=0. As bcsinθ=b×c and b∣∣c, so θ=0. Therefore, b×c=0. And (b×c) vector will be perpendicular to both b and c. So, if a,b,c are in same plane then a.(b×c)=b(a×c)=c(b×a)=0. As if a⊥b, then a.b=0.
