Question
Question: Let $\overline{p}=4\hat{\imath}-\hat{\jmath}+\hat{k}$, $\overline{q}=11\hat{\imath}-\hat{\jmath}+\ha...
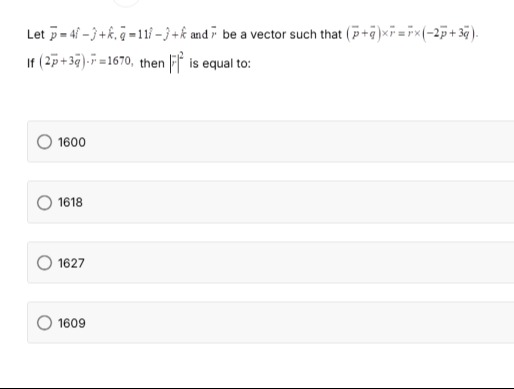
Let p=4^−^+k^, q=11^−^+k^ and r be a vector such that (p+q)×r=r×(−2p+3q). If (2p+3q)⋅r=1670, then ∣r∣2 is equal to:
A
1600
B
1618
C
1627
D
1609
Answer
1618
Explanation
Solution
The first condition (p+q)×r=r×(−2p+3q) simplifies to (−p+4q)×r=0, implying r is parallel to −p+4q. Thus, r=k(−p+4q). Calculating −p+4q=40^−3^+3k^. The second condition (2p+3q)⋅r=1670 is used to find k. Calculating 2p+3q=41^−5^+5k^. Substituting r=k(40^−3^+3k^) into the dot product gives k(41^−5^+5k^)⋅(40^−3^+3k^)=1670, which simplifies to k(1640+15+15)=1670, so 1670k=1670, leading to k=1. Therefore, r=40^−3^+3k^. Finally, ∣r∣2=402+(−3)2+32=1600+9+9=1618.
