Solveeit Logo
Login

Question

Question: Let \(\overline{a},\overline{b},\overline{c},\overline{d}\) be position vectors of four points A, B,...

Let a‾,b‾,c‾,d‾\overline{a},\overline{b},\overline{c},\overline{d} be position vectors of four points A, B, C and D lying in a plane. If (a‾−d‾).(b‾−c‾)=0=(b‾−d‾).(c‾−a‾)\left( \overline{a}-\overline{d} \right).\left( \overline{b}-\overline{c} \right)=0=\left( \overline{b}-\overline{d} \right).\left( \overline{c}-\overline{a} \right) , then ΔABC\Delta ABC has D as:
(a) in-centre
(b) circum-centre
(c) ortho-centre
(d) centroid

Explanation

Solution

We know that if the dot product of two vectors is 0 this means that the two vectors are perpendicular to each other. And it is given that if ABC is a triangle then we are asked about the point D. As you can see that point D (or d‾)\left( or\text{ }\overline{\text{d}} \right) has occurred in both the dot products given in the above problem so the point D will lie inside the triangle ABC.

Complete step by step answer:
In the above problem, it is given that from the three position vectors with points A, B and C, a triangle has been constructed and the point D lies inside the circle.

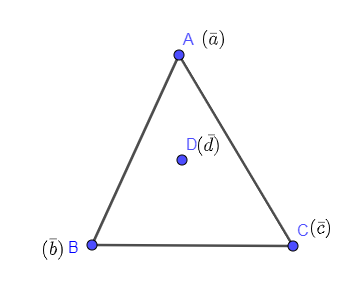
Also, there is a relation between the vectors a‾,b‾,c‾,d‾\overline{a},\overline{b},\overline{c},\overline{d} which we are shown below:
(a‾−d‾).(b‾−c‾)=0=(b‾−d‾).(c‾−a‾)\left( \overline{a}-\overline{d} \right).\left( \overline{b}-\overline{c} \right)=0=\left( \overline{b}-\overline{d} \right).\left( \overline{c}-\overline{a} \right)
We know that when the two vectors are perpendicular to each other then their dot product is 0 so the vectors (a‾−d‾)&(b‾−c‾)\left( \overline{a}-\overline{d} \right)\And \left( \overline{b}-\overline{c} \right) are perpendicular to each other. Also the vectors (b‾−d‾)&(c‾−a‾)\left( \overline{b}-\overline{d} \right)\And \left( \overline{c}-\overline{a} \right) are perpendicular to each other.
Now, we can write (a‾−d‾)\left( \overline{a}-\overline{d} \right) as AD and (b‾−c‾)\left( \overline{b}-\overline{c} \right) as BC and (b‾−d‾)\left( \overline{b}-\overline{d} \right) as BD and (c‾−a‾)\left( \overline{c}-\overline{a} \right) as CA. Drawing these vectors in the given triangle. Also, make sure that the vectors whose dot product is 0 are perpendicular to each other.

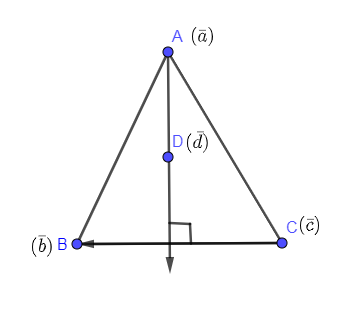
In the above problem we have drawn (a‾−d‾)&(b‾−c‾)\left( \overline{a}-\overline{d} \right)\And \left( \overline{b}-\overline{c} \right).
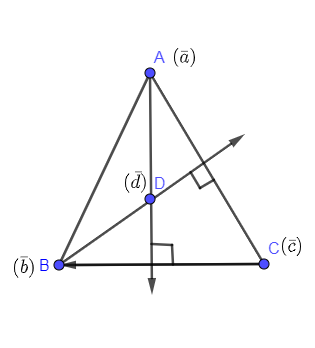
Now, drawing (b‾−d‾)&(c‾−a‾)\left( \overline{b}-\overline{d} \right)\And \left( \overline{c}-\overline{a} \right) we get,

We know that orthocenter is the point in the triangle which is the intersection of all the altitudes passing through three vertices of the triangle. This means point D is the orthocenter of the triangle.
So, the correct answer is “Option c”.

Note: In the above problem, we have learnt that when the dot product of two vectors is 0 then those two vectors are perpendicular to each other. Also, we have learnt that intersection of altitudes of the three vertices of a triangle is the orthocenter.