Question
Question: Let $\omega$ be a complex number such that $\left|\frac{\omega-i}{\omega+3i}\right|=1$ (where $i=\sq...
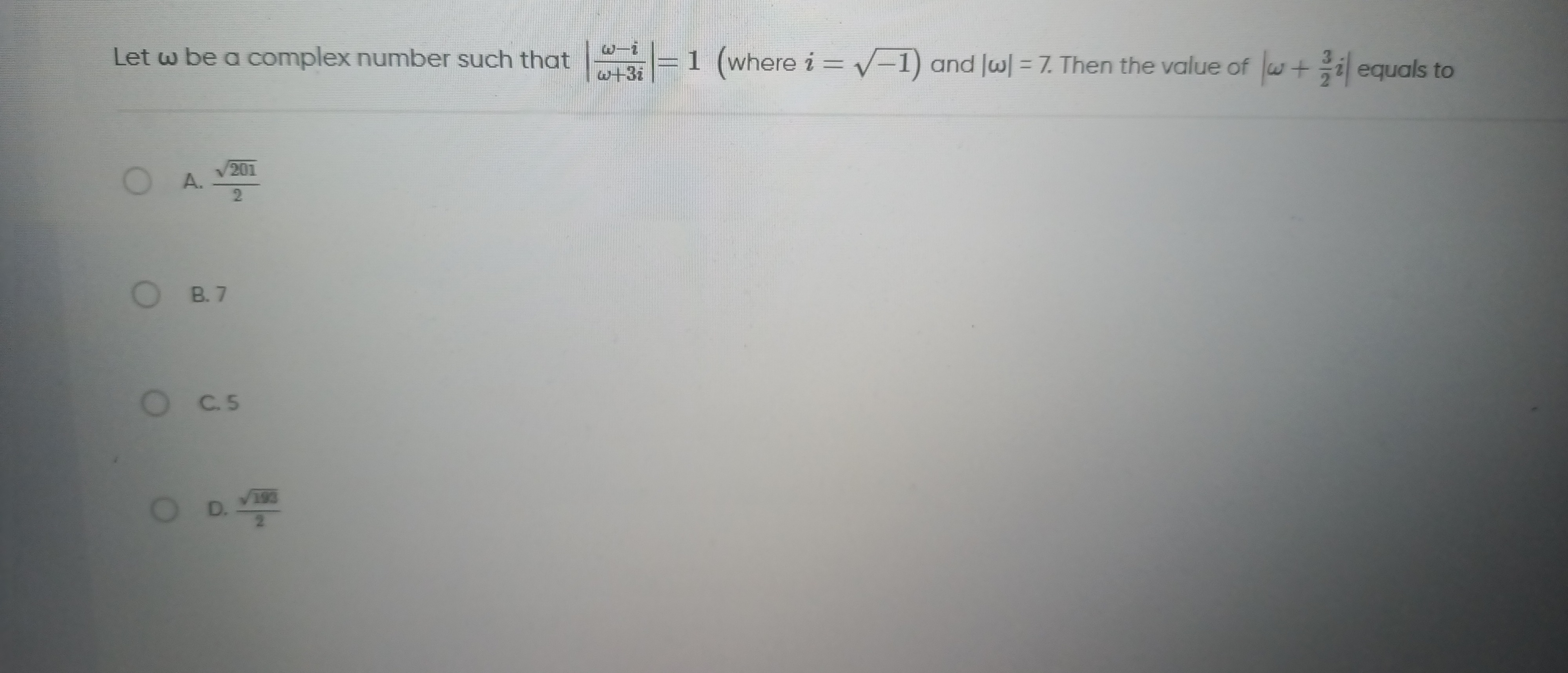
Let ω be a complex number such that ω+3iω−i=1 (where i=−1) and ∣ω∣=7. Then the value of ω+23i equals to
A
2201
B
7
C
5
D
2193
Answer
2193
Explanation
Solution
Let ω=x+iy. The condition ω+3iω−i=1 implies ∣ω−i∣2=∣ω+3i∣2. ∣x+i(y−1)∣2=∣x+i(y+3)∣2 x2+(y−1)2=x2+(y+3)2 y2−2y+1=y2+6y+9 −2y+1=6y+9 8y=−8 y=−1.
The condition ∣ω∣=7 implies ∣ω∣2=49. x2+y2=49 Substituting y=−1: x2+(−1)2=49 x2+1=49 x2=48.
We need to find ω+23i. Substitute ω=x+iy=x−i: x−i+23i=x+i(21) This is equal to x2+(21)2. Substitute x2=48: 48+41=4192+1=4193=2193.
