Question

Let O be the origin, and OX, OY, OZ be three unit vectors in the direction of the sides QR, RP, PQ, respectively of a triangle PQR. $\left| OX\times OY \right|$ =
(a) sin (P + R)
(b) sin 2R
(c) sin (Q + R)
(d) sin (P + Q)

Answer 1

First of all, we will draw the figure of triangle PQR. We will also draw the unit vectors in the directions as mentioned in the question. Then, we are asked to find the modulus of cross product of vector OX and vector OY represented as$\left| OX\times OY \right|$. To find this cross product, we will first define the cross product of any two vectors. We will refer to the figure whenever necessary for additional information.

Complete step-by-step answer:
It is given to us that O is the origin and OX, OY, OZ are the 3 unit vectors in the direction of the sides QR, RP, PQ, respectively of a triangle PQR.
Thus, we will use this information to draw a figure of the triangle and the vectors.
The figure is as follows:

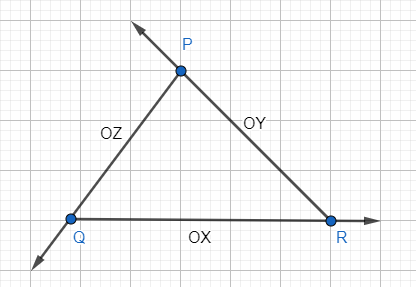
The value of the internal angles at vertices P, Q and R is P, Q and R respectively.
Now, we are supposed to find the value of the modulus of cross product of vector OX and vector OY represented as $\left| OX\times OY \right|$.
Now, suppose if a and b are any two vectors, then the cross product is defined as the product of their magnitudes and sine of angle between them. In mathematical representation, it is given as $\left| a\times b \right|=\left| a \right|\left| b \right|\sin \theta$.
$\Rightarrow \left| OX\times OY \right|=\left| OX \right|\left| OY \right|\sin \theta$
Now, it is given to use that OX, OY and OZ are three unit vectors. This means the magnitude of each of OX, OY and OZ is 1.

& \Rightarrow \left| OX\times OY \right|=\left( 1 \right)\left( 1 \right)\sin \theta \\\ & \Rightarrow \left| OX\times OY \right|=\sin \theta \\\ \end{aligned}$$ From the figure, we can see that angle between the OX and OY is the external angle of the triangle at vertex R. We also know that the external angle and the internal angle at the same vertex of a triangle are supplementary. Which means, the sum of the angles is 180°. Therefore, the external angle at R = $\theta $ = 180° ─ R We also know that the sum of the internal angles of a triangle is 180°. Therefore, $\theta $ = P + Q + R ─ R = P + Q $$\Rightarrow \left| OX\times OY \right|=\sin \left( P+Q \right)$$ **So, the correct answer is “Option d”.** **Note:** Figure was of utmost importance in this question. The internal and external angle could only be understood with the help of figure. This problem requires the basics of vector algebra as well as geometry.