Question

Let $O$ be the centre of the circle ${x^2} + {y^2} = {r^2}$ , where $r > \dfrac{{\sqrt 5 }}{2}$ . Suppose PQ is a chord of this circle and the equation of the line passing through P and Q is $2x + 4y = 5$ . If the centre of the circumcircle of the triangle OPQ lies on the line $x + 2y = 4$ , then the value of $r$ is ________.

Answer 1

In the above given problem, we are given a circle with centre O which has a chord PQ. There is another circle which is the circumcircle of the triangle OPQ, whose centre lies on a given line. The equation of the chord and the line is given. We have to find the radius of the circle O, where $r > \dfrac{{\sqrt 5 }}{2}$.

Complete step by step answer:
Let us first draw the diagram of the required circles according to the information given in the above question. That will provide the following diagram is drawn below.

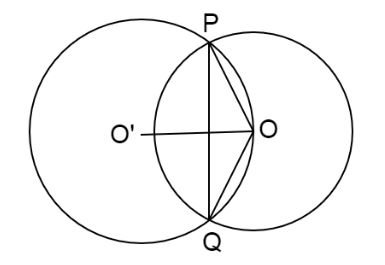
Now, the equation o the circle O is ${x^2} + {y^2} = {r^2}$ , where $r > \dfrac{{\sqrt 5 }}{2}$. Here the centre of the circle O is the origin, i.e. $\left( {0,0} \right)$. Now, let the equation of the circle O’ be ${x^2} + {y^2} + ax + by = 0$. That gives the centre of the circle O’ as $\left( { - \dfrac{a}{2}, - \dfrac{b}{2}} \right)$.

Now, since the radical axis of these two circles is PQ. Therefore, the equation of PQ will be given by the difference of equations of the two circles, i.e.
$\Rightarrow PQ:O - O'$
i.e.
$\Rightarrow PQ:ax + by + {r^2} = 0$
But it is given that the equation of PQ is $2x + 4y = 5$ i.e.
$\Rightarrow PQ:2x + 4y - 5 = 0$
Therefore, comparing the two equations, we get
$\Rightarrow \dfrac{a}{2} = \dfrac{b}{4} = \dfrac{{{r^2}}}{{ - 5}}$
That gives us,
$\Rightarrow a = - \dfrac{{2{r^2}}}{5},b = - \dfrac{{4{r^2}}}{5}$

Therefore, the centre of O’ is,
$\Rightarrow O':\left( { - \dfrac{a}{2}, - \dfrac{b}{2}} \right) = \left( {\dfrac{{{r^2}}}{5},\dfrac{{2{r^2}}}{5}} \right)$
Since, the centre O’ lies on the line $x + 2y = 4$
Therefore we have
$\Rightarrow \dfrac{{{r^2}}}{5} + 2 \cdot \dfrac{{2{r^2}}}{5} = 4$
That gives,
$\Rightarrow 5{r^2} = 20$
$\Rightarrow {r^2} = 4$
Since radius is always positive, hence
$\therefore r = 2$

Therefore the radius of the circle is $2$.

Note: The radical axis of two circles is the locus of a point from which the tangent segments to the two circles are of equal lengths. The radical axis can be the common chord to both the circles if they are partially inscribed in each other. Otherwise, if the two circles touch each other at exactly one point, then the radical axis is the common tangent to both the circles at that point.