Question
Question: Let $n = 75600$, then find the value of $\frac{4}{log_2 n} + \frac{3}{log_3 n} + \frac{2}{log_5 n} +...
Let n=75600, then find the value of log2n4+log3n3+log5n2+log7n1
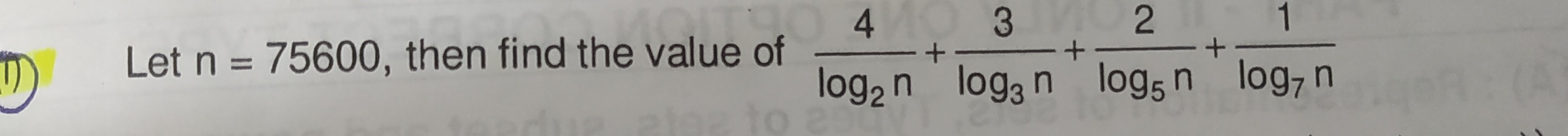
1
Solution
Let the given expression be E. We are given n=75600. We first find the prime factorization of n. n=75600=756×100 756=2×378=22×189=22×3×63=22×3×32×7=22×33×71 100=102=(2×5)2=22×52 So, n=(22×33×71)×(22×52)=22+2×33×52×71=24×33×52×71.
The given expression is E=log2n4+log3n3+log5n2+log7n1. Using the change of base formula for logarithms, logba1=logab, we can rewrite each term: log2n1=logn2 log3n1=logn3 log5n1=logn5 log7n1=logn7
Substitute these into the expression E: E=4×logn2+3×logn3+2×logn5+1×logn7
Using the logarithm property k×logba=logbak, we get: E=logn24+logn33+logn52+logn71
Using the logarithm property logbx+logby+logbz+...=logb(x×y×z×...), we can combine the terms: E=logn(24×33×52×71)
From the prime factorization of n, we know that n=24×33×52×71. So, the expression becomes: E=lognn
Using the logarithm property logbb=1, we have: E=1
