Question

Let M = [$a_{uv}$]$_{nxn}$ be a square matrix of order n where $a_{uv}$ = sin ($\theta_u$-$\theta_v$) + i cos($\theta_u$-$\theta_v$), then M is equal to (where $\overline{M}$ and $M^T$ are conjugate of M and transpose of M respectively.) Q.1

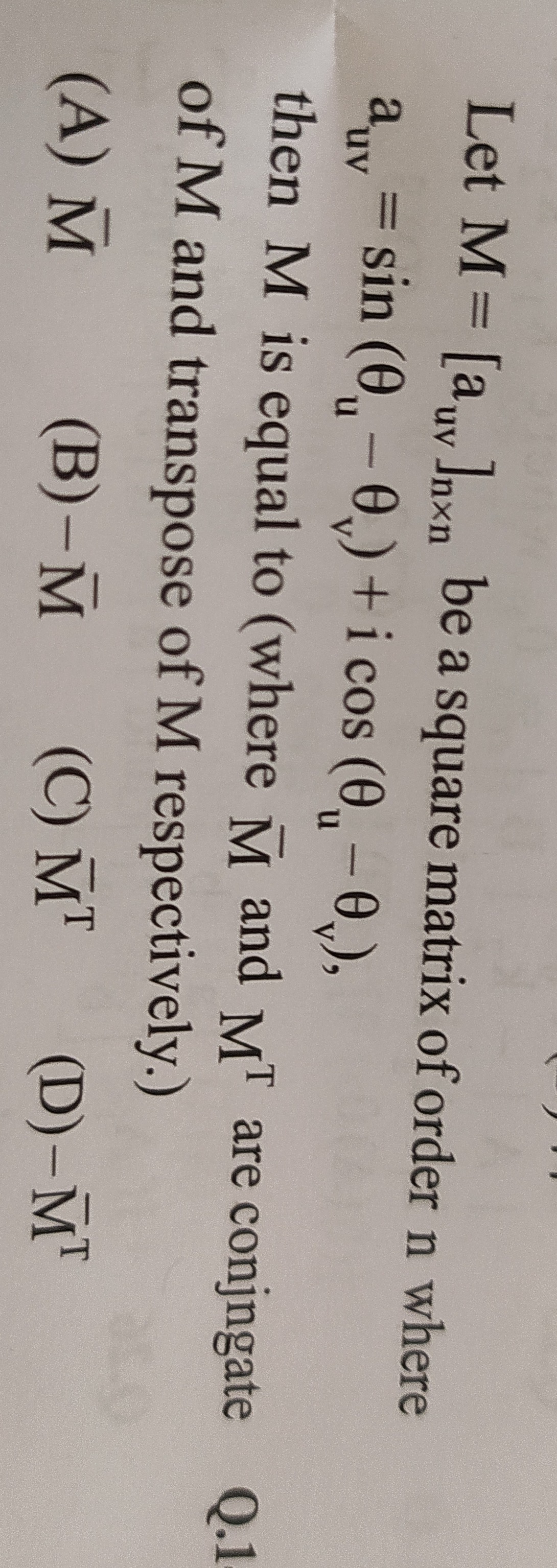
• A. $\overline{M}$
• B. -$\overline{M}$
• C. $\overline{M}^T$
• D. -$\overline{M}^T$

Answer 1

Answer: (D)

-$\overline{M}^T$

Answer 2

Let the matrix M be given by $M = [a_{uv}]_{nxn}$, where $a_{uv} = \sin(\theta_u - \theta_v) + i \cos(\theta_u - \theta_v)$.

We can rewrite the element $a_{uv}$ using the identity $\cos x - i \sin x = e^{-ix}$.

$a_{uv} = \sin(\theta_u - \theta_v) + i \cos(\theta_u - \theta_v)$

Factor out $i$:

$a_{uv} = i \left( \frac{\sin(\theta_u - \theta_v)}{i} + \cos(\theta_u - \theta_v) \right)$

Since $\frac{1}{i} = -i$:

$a_{uv} = i \left( -i \sin(\theta_u - \theta_v) + \cos(\theta_u - \theta_v) \right)$

$a_{uv} = i \left( \cos(\theta_u - \theta_v) - i \sin(\theta_u - \theta_v) \right)$

Using Euler's formula $e^{-ix} = \cos x - i \sin x$:

$a_{uv} = i e^{-i(\theta_u - \theta_v)}$

$a_{uv} = i e^{-i\theta_u} e^{i\theta_v}$.

Now let's consider the transpose of M, denoted by $M^T$. The element $(M^T)_{uv}$ is $a_{vu}$.

$a_{vu} = \sin(\theta_v - \theta_u) + i \cos(\theta_v - \theta_u)$.

Using the properties $\sin(-x) = -\sin x$ and $\cos(-x) = \cos x$:

$a_{vu} = \sin(-(\theta_u - \theta_v)) + i \cos(-(\theta_u - \theta_v))$

$a_{vu} = -\sin(\theta_u - \theta_v) + i \cos(\theta_u - \theta_v)$.

Next, consider the complex conjugate of $M^T$, denoted by $\overline{M}^T$. The element $(\overline{M}^T)_{uv}$ is the complex conjugate of $(M^T)_{uv}$, which is $\overline{a_{vu}}$.

$\overline{a_{vu}} = \overline{-\sin(\theta_u - \theta_v) + i \cos(\theta_u - \theta_v)}$

$\overline{a_{vu}} = -\sin(\theta_u - \theta_v) - i \cos(\theta_u - \theta_v)$.

Finally, consider the matrix $-\overline{M}^T$. The element $(-\overline{M}^T)_{uv}$ is $-(\overline{M}^T)_{uv}$, which is $-\overline{a_{vu}}$.

$(-\overline{M}^T)_{uv} = -(-\sin(\theta_u - \theta_v) - i \cos(\theta_u - \theta_v))$

$(-\overline{M}^T)_{uv} = \sin(\theta_u - \theta_v) + i \cos(\theta_u - \theta_v)$.

This result is exactly equal to the element $a_{uv}$.

So, $a_{uv} = (-\overline{M}^T)_{uv}$ for all $u, v$.

Therefore, the matrix M is equal to $-\overline{M}^T$.

$M = -\overline{M}^T$.

This means M is a skew-Hermitian matrix.