Solveeit Logo
Login

Question

Question: Let line passing through A (1,-1,1) which intersect the lines $x+y+1=0, z=0$ and $x-y=1, y+z=2$ is p...

Let line passing through A (1,-1,1) which intersect the lines x+y+1=0,z=0x+y+1=0, z=0 and x−y=1,y+z=2x-y=1, y+z=2 is parallel to

A

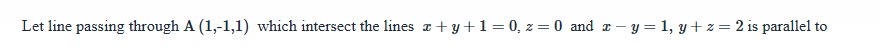
(0,1,1)(0, 1, 1)

B

(1,0,1)(1, 0, 1)

C

(1,1,0)(1, 1, 0)

D

(0,−1,−1)(0, -1, -1)

Answer

(0, 1, 1)

Explanation

Solution

Let the given point be A=(1,−1,1)A = (1, -1, 1).

The first line, L1L_1, is given by the equations: x+y+1=0x + y + 1 = 0 z=0z = 0 Parametric form of L1L_1: Let y=ty = t. Then x=−t−1x = -t - 1 and z=0z = 0. A point PP on L1L_1 is P(t)=(−t−1,t,0)P(t) = (-t-1, t, 0).

The second line, L2L_2, is given by the equations: x−y=1x - y = 1 y+z=2y + z = 2 Parametric form of L2L_2: Let y=sy = s. Then x=s+1x = s + 1 and z=2−sz = 2 - s. A point QQ on L2L_2 is Q(s)=(s+1,s,2−s)Q(s) = (s+1, s, 2-s).

Let the line passing through point AA be LL. LL intersects L1L_1 at PP and L2L_2 at QQ. Thus, A,P,QA, P, Q are collinear. The direction vector of LL can be AP⃗\vec{AP} or AQ⃗\vec{AQ}.

AP⃗=P(t)−A=(−t−1−1,t−(−1),0−1)=(−t−2,t+1,−1)\vec{AP} = P(t) - A = (-t-1 - 1, t - (-1), 0 - 1) = (-t-2, t+1, -1) AQ⃗=Q(s)−A=(s+1−1,s−(−1),2−s−1)=(s,s+1,1−s)\vec{AQ} = Q(s) - A = (s+1 - 1, s - (-1), 2-s - 1) = (s, s+1, 1-s)

Since A,P,QA, P, Q are collinear, AP⃗\vec{AP} and AQ⃗\vec{AQ} are parallel: −t−2s=t+1s+1=−11−s\frac{-t-2}{s} = \frac{t+1}{s+1} = \frac{-1}{1-s}

From t+1s+1=−11−s\frac{t+1}{s+1} = \frac{-1}{1-s}: (t+1)(1−s)=−(s+1)(t+1)(1-s) = -(s+1) t−ts+1−s=−s−1t - ts + 1 - s = -s - 1 t+1=ts−1t + 1 = ts - 1 t−ts=−2t - ts = -2 t(1−s)=−2(∗)t(1-s) = -2 \quad (*)

From −t−2s=−11−s\frac{-t-2}{s} = \frac{-1}{1-s}: (−t−2)(1−s)=−s(-t-2)(1-s) = -s −t+ts−2+2s=−s-t + ts - 2 + 2s = -s ts−t=2−3sts - t = 2 - 3s t(s−1)=2−3st(s-1) = 2 - 3s

Let's re-solve using the first and third ratios: −t−2s=−11−s\frac{-t-2}{s} = \frac{-1}{1-s} (−t−2)(1−s)=−s(-t-2)(1-s) = -s −t+ts−2+2s=−s-t + ts - 2 + 2s = -s ts−t+3s−2=0ts - t + 3s - 2 = 0

And the second and third ratios: t+1s+1=−11−s\frac{t+1}{s+1} = \frac{-1}{1-s} (t+1)(1−s)=−(s+1)(t+1)(1-s) = -(s+1) t−ts+1−s=−s−1t - ts + 1 - s = -s - 1 t−ts=−2t - ts = -2 t(1−s)=−2(∗)t(1-s) = -2 \quad (*)

Substitute t=−21−st = \frac{-2}{1-s} into the equation from the first and third ratios: (−21−s)s−(−21−s)+3s−2=0(\frac{-2}{1-s})s - (\frac{-2}{1-s}) + 3s - 2 = 0 −2s1−s+21−s+3s−2=0\frac{-2s}{1-s} + \frac{2}{1-s} + 3s - 2 = 0 −2s+21−s+3s−2=0\frac{-2s+2}{1-s} + 3s - 2 = 0 −2(s−1)−(s−1)+3s−2=0\frac{-2(s-1)}{-(s-1)} + 3s - 2 = 0 2+3s−2=02 + 3s - 2 = 0 3s=0  ⟹  s=03s = 0 \implies s = 0

Substitute s=0s=0 into t(1−s)=−2t(1-s) = -2: t(1−0)=−2  ⟹  t=−2t(1-0) = -2 \implies t = -2.

Now find the direction vector using t=−2t=-2 in AP⃗\vec{AP}: AP⃗=(−(−2)−2,−2+1,−1)=(2−2,−1,−1)=(0,−1,−1)\vec{AP} = (-(-2)-2, -2+1, -1) = (2-2, -1, -1) = (0, -1, -1). Alternatively, using s=0s=0 in AQ⃗\vec{AQ}: AQ⃗=(0,0+1,1−0)=(0,1,1)\vec{AQ} = (0, 0+1, 1-0) = (0, 1, 1).

The direction vector is parallel to (0,1,1)(0, 1, 1).