Solveeit Logo
Login

Question

Question: Let $$ f(x) = \begin{cases} \frac{a(1-x\sin x)+b\cos x+5}{x^2}, & x<0 \\ 3, & x=0. \\ \left(1+\left(...

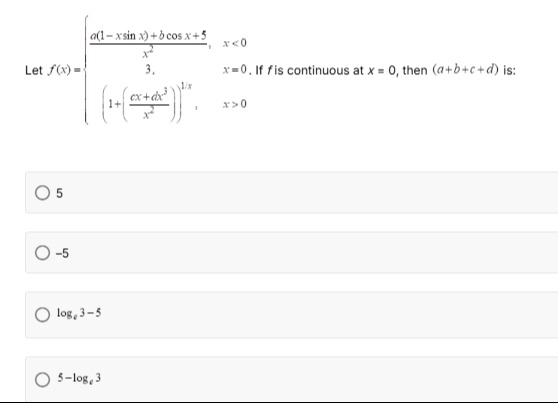
Let

f(x)={a(1−xsin⁡x)+bcos⁡x+5x2,x<03,x=0.(1+(cx+dx3x2))1/x,x>0f(x) = \begin{cases} \frac{a(1-x\sin x)+b\cos x+5}{x^2}, & x<0 \\ 3, & x=0. \\ \left(1+\left(\frac{cx+dx^3}{x^2}\right)\right)^{1/x}, & x>0 \end{cases}

If ff is continuous at x=0x=0, then (a+b+c+d)(a+b+c+d) is:

A

ln⁡3−5\ln 3 - 5

B

5−ln⁡35 - \ln 3

C

−5+ln⁡3-5 + \ln 3

D

−5−ln⁡3-5 - \ln 3

Answer

ln⁡3−5\ln 3 - 5

Explanation

Solution

For the function f(x)f(x) to be continuous at x=0x=0, the left-hand limit, the right-hand limit, and the function value at x=0x=0 must be equal. We are given f(0)=3f(0) = 3.

1. Left-hand limit: lim⁡x→0−f(x)=lim⁡x→0−a(1−xsin⁡x)+bcos⁡x+5x2\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} \frac{a(1-x\sin x)+b\cos x+5}{x^2} For the limit to be finite, the numerator must approach 0 as x→0x \to 0. As x→0x \to 0, a(1−xsin⁡x)+bcos⁡x+5→a(1−0)+b(1)+5=a+b+5a(1-x\sin x)+b\cos x+5 \to a(1-0) + b(1) + 5 = a+b+5. So, we must have a+b+5=0a+b+5 = 0, which implies a+b=−5a+b = -5.

Using Taylor series expansions: sin⁡x≈x\sin x \approx x and cos⁡x≈1−x22\cos x \approx 1 - \frac{x^2}{2}. Numerator ≈a(1−x2)+b(1−x22)+5=(a+b+5)−(a+b2)x2\approx a(1 - x^2) + b(1 - \frac{x^2}{2}) + 5 = (a+b+5) - (a + \frac{b}{2})x^2. Since a+b+5=0a+b+5=0, the numerator is −(a+b2)x2- (a + \frac{b}{2})x^2. The left-hand limit is: lim⁡x→0−−(a+b2)x2x2=−(a+b2)\lim_{x \to 0^-} \frac{- (a + \frac{b}{2})x^2}{x^2} = - (a + \frac{b}{2}) For continuity, −(a+b2)=3- (a + \frac{b}{2}) = 3, which means a+b2=−3a + \frac{b}{2} = -3.

Solving the system:

  1. a+b=−5a+b = -5
  2. a+b2=−3a + \frac{b}{2} = -3 Subtracting (2) from (1): b2=−2  ⟹  b=−4\frac{b}{2} = -2 \implies b = -4. Substituting b=−4b=-4 into (1): a−4=−5  ⟹  a=−1a - 4 = -5 \implies a = -1.

2. Right-hand limit: lim⁡x→0+f(x)=lim⁡x→0+(1+(cx+dx3x2))1/x=lim⁡x→0+(1+cx+dx)1/x\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} \left(1+\left(\frac{cx+dx^3}{x^2}\right)\right)^{1/x} = \lim_{x \to 0^+} \left(1+\frac{c}{x}+dx\right)^{1/x} For the limit to be finite, we must have c=0c=0. The limit becomes lim⁡x→0+(1+dx)1/x\lim_{x \to 0^+} (1+dx)^{1/x}. This is of the form 1∞1^\infty. Using the standard limit lim⁡x→0(1+kx)1/x=ek\lim_{x \to 0} (1+kx)^{1/x} = e^k, we get ede^d.

For continuity, ed=3e^d = 3, so d=ln⁡3d = \ln 3.

3. Sum of coefficients: a=−1a = -1, b=−4b = -4, c=0c = 0, d=ln⁡3d = \ln 3. a+b+c+d=−1+(−4)+0+ln⁡3=−5+ln⁡3a+b+c+d = -1 + (-4) + 0 + \ln 3 = -5 + \ln 3.