Question

Let $\langle a_n \rangle$ be a sequence such that $a_0 = 0, a_1 = \frac{1}{2}$ and $2a_{n+2} = 5a_{n+1} - 3a_n, n = 0, 1, 2, 3, \dots$ Then is equal to

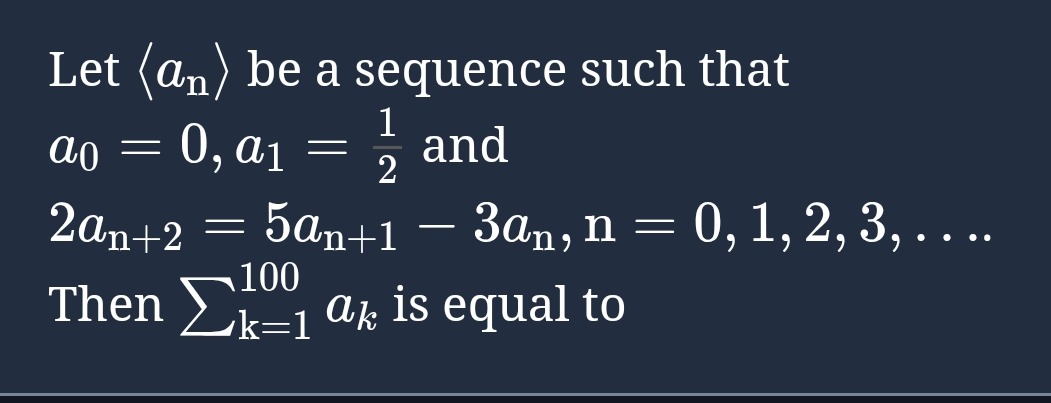
Answer 1

3\left(\frac{3}{2}\right)^{100} - 103

Answer 2

Solution Explanation:

1. Write the recurrence as:
     2aₙ₊₂ − 5aₙ₊₁ + 3aₙ = 0
2. The characteristic equation is:
     2r² − 5r + 3 = 0
     Factorizing gives: (2r − 3)(r − 1) = 0, so r = 3/2 and r = 1.
3. Hence, the general solution is:
     aₙ = A(3/2)ⁿ + B(1)ⁿ = A(3/2)ⁿ + B
4. Use initial conditions:
     a₀ = 0 ⇒ A + B = 0  ⟹  B = −A
     a₁ = ½ ⇒ A(3/2 − 1) = ½  ⟹  A(½) = ½  ⟹  A = 1
     Thus, aₙ = (3/2)ⁿ − 1.
5. The sum from k = 1 to 100 is:
     S = Σₖ₌₁¹⁰⁰ aₖ = Σₖ₌₁¹⁰⁰[(3/2)ᵏ − 1]
       = Σₖ₌₁¹⁰⁰ (3/2)ᵏ − 100
6. Sum the geometric series:
     Σₖ₌₁¹⁰⁰ (3/2)ᵏ = (3/2)·[((3/2)¹⁰⁰ − 1)/((3/2) − 1)]
     Since (3/2) − 1 = ½, we have:
       = (3/2)·[((3/2)¹⁰⁰ − 1)/(½)]
       = 3·[(3/2)¹⁰⁰ − 1]
7. Therefore, S = 3[(3/2)¹⁰⁰ − 1] − 100 = 3(3/2)¹⁰⁰ − 3 − 100 = 3(3/2)¹⁰⁰ − 103.