Question

Let L be the line passing through the points P (1, 2) such that its intercepted segment between the coordinates axes is bisected at P. If ${L_1}$ is the line perpendicular to L and passing through the point (-2, 1), then the point of intersection of L and ${L_1}$ is:
A. $\left( {\dfrac{4}{5},\dfrac{{12}}{5}} \right)$
B. $\left( {\dfrac{{11}}{{20}},\dfrac{{29}}{{10}}} \right)$
C. $\left( {\dfrac{3}{{10}},\dfrac{{17}}{5}} \right)$
D. $\left( {\dfrac{3}{5},\dfrac{{23}}{{10}}} \right)$

Answer 1

Hint : We have the equation of line passing through point we have $({x_0},{y_0})$ and slope $m$ is $y - {y_0} = m(x - {x_0})$ . We also know the equation of intercept is $\dfrac{x}{a} + \dfrac{y}{b} = 1$ . Now we need to find $(x,y)$ . We first find the values of ‘a’ and ‘b’ by the condition of the intercepted segment. We also know that if two lines are perpendicular then the product of their slope is -1.

Complete step-by-step answer :
Let the equation of line of intercept is
$\dfrac{x}{a} + \dfrac{y}{b} = 1$
Line cut X-axis at $A(a,0)$ and Y-axis at $B(0.b)$ .

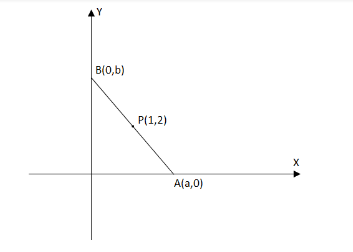
Since the intercept segment between the axes is bisected at P. So coordinate of P are $P\left( {\dfrac{a}{2},\dfrac{b}{2}} \right)$ .
But coordinates of P are given, $P(1,2)$ .
Comparing these two and equating ‘X’ and ‘Y’ coordinates we have:
$\Rightarrow \dfrac{a}{2} = 1$ and $\Rightarrow \dfrac{b}{2} = 2$ .
$\Rightarrow a = 2$ and $\Rightarrow b = 4$ .
Now, equation of line is given by,
$\Rightarrow \dfrac{x}{2} + \dfrac{y}{4} = 1$
Taking L.C.M. we have,
$\Rightarrow \dfrac{{2x + y}}{4} = 1$
$\Rightarrow 2x + y = 4{\text{ - - - - - (1)}}$
Rearranging we have, $y = - 2x + 4$
Comparing this with $y = mx + c$ we have, $m = - 2$ .
Since ${L_1}$ is perpendicular to L.
Slope of line $\Rightarrow {L_1} = \dfrac{1}{2}$ .
Equation of ${L_1} = \dfrac{1}{2}$ passing through (-2, 1) is
$\Rightarrow y - 1 = \dfrac{1}{2}(x + 2)$
$\Rightarrow y - 1 = \dfrac{x}{2} + 1$
Taking L.C.M. we have,
$\Rightarrow (y - 1) = \dfrac{{x + 2}}{2}$
Multiply by 2 on both sides we have,
$\Rightarrow 2(y - 1) = x + 2$
$\Rightarrow 2y - 2 = x + 2$
$\Rightarrow 2y - x = 4{\text{ - - - - - (2)}}$
Now solving equation (1) and (2), we will get the intercept points.
From (2) we have $x = 2y - 4{\text{ - - - - (3)}}$ and substituting in equation (1) we have,
$\Rightarrow 2\left( {2y - 4} \right) + y = 4{\text{ }}$
$\Rightarrow 4y - 8 + y = 4$
$\Rightarrow 5y = 4 + 8$
$\Rightarrow 5y = 12$
$\Rightarrow y = \dfrac{{12}}{5}.$
Now substituting ‘y’ in equation (3) we have,
$\Rightarrow x = 2\left( {\dfrac{{12}}{5}} \right) - 4$
$\Rightarrow x = \dfrac{{24}}{5} - 4$
Taking 5 as L.C.M.
$\Rightarrow x = \dfrac{{24 - 20}}{5}$
$\Rightarrow x = \dfrac{4}{5}$ .
Thus we have the point of intersection of L and ${L_1}$ is $\left( {\dfrac{4}{5},\dfrac{{12}}{5}} \right)$ .
So, the correct answer is “Option A”.

Note : Remember the equation of intercepts of equations. We also know if two equations are perpendicular then their product of slopes is -1, that is ${m_1} \times {m_2} = - 1$ . Using this we found the slope of ${L_1}$ . Which is perpendicular to L. We have solved the above two equations by substituting. We can also solve this by elimination and cross product method.