Question
Question: Let \[{L_1}\] be the length of the common chord of curves \[{x^2} + {y^2} = 9\] and \[{y^2} = 8x\], ...
Let L1 be the length of the common chord of curves x2+y2=9 and y2=8x, and let L2 be the length of the latus rectum of y2=8x, then:
A. L1<L2
B. L1L1=2
C. L1>L2
D. L1=L2
Solution
Here we draw both parabola and circle on the graph and find their point of intersection. Then joining the two points we can find the length of the common chord. Comparing the equation of parabola we find the length of the latus rectum using the formula and compare the lengths.
- Length between two points (x1,y1);(x2,y2) is given by (x1−x2)2+(y1−y2)2
- Length of latus rectum of a parabola y2=4ax is given by 4a
Complete step-by-step answer:
We have the curves x2+y2=9 and y2=8x . We can see that the equation x2+y2=9 is the equation of the circle and the equation y2=8x is the equation of a parabola.
Then we can roughly draw the two curves
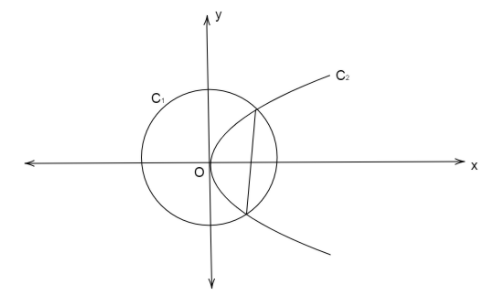
C1 represents the circle x2+y2=9 and C2 represents the parabola y2=8x.
We find the points of intersection of circle and the parabola.
Substitute the value of y2=8x in equation x2+y2=9
⇒x2+8x=9
Shift all the values to one side of the equation
⇒x2+8x−9=0
Breaking the middle term to factorize the equation
⇒x2−x+9x−9=0
Taking x common from first two terms and 9 common from last two terms.
So, equating the factors equal to zero
⇒(x−1)(x+9)=0
Since from the diagram we see the points of intersection are on the positive x –axis, so we ignore the value of x that is negative.
⇒x=1
Now we substitute the value of x in equation of parabola to find the value of y
Writing the constant term in form of square of a number
⇒y2=(22)2
Taking square root on both sides
⇒y2=(22)2
Cancel square root with square power
⇒y=±22
So, the two points are (1,22),(1,−22).
Now we calculate the length L1 between the two points (1,22),(1,−22) using the formula (x1−x2)2+(y1−y2)2, where x1=1,y1=22,x2=1,y2=−22
Cancel out square from under root
⇒L1=42 … (1)
Now we use the formula for latus rectum of parabola.
Comparing the equation of parabola y2=8x to general equation of parabola y2=4ax
Now the length of latus rectum
⇒L2=4a ⇒L2=4×2 ⇒L2=8Comparing the values of L1=42,L2=8, we see that L1<L2
So, the correct answer is “Option A”.
Note: Students are likely to make mistakes while finding the value of a by comparing the equation of parabola to the general equation of parabola as they write the complete value of a as 8 which is wrong.
