Solveeit Logo
Login

Question

Question: Let \({{L}_{1}}\And {{L}_{2}}\) denote the lines \(\overrightarrow{r}=\overset{\wedge }{\mathop{i}}\...

Let L1&L2{{L}_{1}}\And {{L}_{2}} denote the lines r→=i∧ +λ(−i∧ +2j∧ +2k∧ ),λ∈R\overrightarrow{r}=\overset{\wedge }{\mathop{i}}\,+\lambda \left( -\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+2\overset{\wedge }{\mathop{k}}\, \right),\lambda \in R and r→=μ(2i∧ −j∧ +2k∧ ),μ∈R\overrightarrow{r}=\mu \left( 2\overset{\wedge }{\mathop{i}}\,-\overset{\wedge }{\mathop{j}}\,+2\overset{\wedge }{\mathop{k}}\, \right),\mu \in R respectively. If L3{{L}_{3}} is a line which is perpendicular to both L1&L2{{L}_{1}}\And {{L}_{2}} and cut both of them, then which of the following describe(s) L3{{L}_{3}}?
(a) r→=13(2i∧ +k∧ )+t(2i∧ +2j∧ −k∧ ),t∈R\overrightarrow{r}=\dfrac{1}{3}\left( 2\overset{\wedge }{\mathop{i}}\,+\overset{\wedge }{\mathop{k}}\, \right)+t\left( 2\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\, \right),t\in R
(b) r→=29(4i∧ +j∧ +k∧ )+t(2i∧ +2j∧ −k∧ ),t∈R\overrightarrow{r}=\dfrac{2}{9}\left( 4\overset{\wedge }{\mathop{i}}\,+\overset{\wedge }{\mathop{j}}\,+\overset{\wedge }{\mathop{k}}\, \right)+t\left( 2\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\, \right),t\in R
(c) r→=29(2i∧ −j∧ +2k∧ )+t(2i∧ +2j∧ −k∧ ),t∈R\overrightarrow{r}=\dfrac{2}{9}\left( 2\overset{\wedge }{\mathop{i}}\,-\overset{\wedge }{\mathop{j}}\,+2\overset{\wedge }{\mathop{k}}\, \right)+t\left( 2\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\, \right),t\in R
(d) r→=t(2i∧ +2j∧ −k∧ ),t∈R\overrightarrow{r}=t\left( 2\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\, \right),t\in R

Explanation

Solution

We have given the two lines L1&L2{{L}_{1}}\And {{L}_{2}} and it is also given that there is a line L3{{L}_{3}} which is perpendicular to both of these two lines which we are going to find the cross product of the direction ratios of line L1&L2{{L}_{1}}\And {{L}_{2}}. After the cross product calculation, reduce the answer of cross product to the simplest integers then those reduced coefficients of i∧ ,j∧ ,k∧ \overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,,\overset{\wedge }{\mathop{k}}\, are the direction ratios of the lines L3{{L}_{3}}. As you can see that lines L1&L2{{L}_{1}}\And {{L}_{2}} are skew lines so take one point on the line L1{{L}_{1}} and other point on line L2{{L}_{2}} and then find the direction ratios of the two points which is proportional to the one that we solved from the cross product. Then, find the values of the points that you have taken on L1&L2{{L}_{1}}\And {{L}_{2}} and also the midpoint of the two points. This will give you three points. And we can write a line as a→+λb→\overrightarrow{a}+\lambda \overrightarrow{b} so a→\overrightarrow{a} is one of the three points and b→\overrightarrow{b} is the direction ratios of the cross product of the two lines.

Complete step-by-step answer :
We have given the two lines L1&L2{{L}_{1}}\And {{L}_{2}} as follows:
Line L1{{L}_{1}} is given as:
r1→=i∧ +λ(−i∧ +2j∧ +2k∧ ),λ∈R\overrightarrow{{{r}_{1}}}=\overset{\wedge }{\mathop{i}}\,+\lambda \left( -\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+2\overset{\wedge }{\mathop{k}}\, \right),\lambda \in R
Line L2{{L}_{2}} is given as:
r2→=μ(2i∧ −j∧ +2k∧ ),μ∈R\overrightarrow{{{r}_{2}}}=\mu \left( 2\overset{\wedge }{\mathop{i}}\,-\overset{\wedge }{\mathop{j}}\,+2\overset{\wedge }{\mathop{k}}\, \right),\mu \in R
Now, we have to find the line L3{{L}_{3}} such that it is perpendicular to both L1&L2{{L}_{1}}\And {{L}_{2}} so the direction ratio of the line L3{{L}_{3}} is the cross product of the direction ratios of L1&L2{{L}_{1}}\And {{L}_{2}}.
In the following, we have written the direction ratios of lines L1&L2{{L}_{1}}\And {{L}_{2}} as:
L1=(−1,2,2) L2=(2,−1,2) \begin{aligned} & {{L}_{1}}=\left( -1,2,2 \right) \\\ & {{L}_{2}}=\left( 2,-1,2 \right) \\\ \end{aligned}
Now, taking the cross product of L1&L2{{L}_{1}}\And {{L}_{2}} we get,
L1×L2=∣i∧ j∧ k∧  −122 2−12 ∣{{L}_{1}}\times {{L}_{2}}=\left| \begin{matrix} \overset{\wedge }{\mathop{i}}\, & \overset{\wedge }{\mathop{j}}\, & \overset{\wedge }{\mathop{k}}\, \\\ -1 & 2 & 2 \\\ 2 & -1 & 2 \\\ \end{matrix} \right|
Expanding the determinant along the first row we get,
L1×L2=i∧ (2(2)−2(−1))−j∧ (−1(2)−2(2))+k∧ ((−1)(−1)−2(2)) ⇒L1×L2=i∧ (6)−j∧ (−6)+k∧ (−3) ⇒L1×L2=6i∧ +6j∧ −3k∧  \begin{aligned} & {{L}_{1}}\times {{L}_{2}}=\overset{\wedge }{\mathop{i}}\,\left( 2\left( 2 \right)-2\left( -1 \right) \right)-\overset{\wedge }{\mathop{j}}\,\left( -1\left( 2 \right)-2\left( 2 \right) \right)+\overset{\wedge }{\mathop{k}}\,\left( \left( -1 \right)\left( -1 \right)-2\left( 2 \right) \right) \\\ & \Rightarrow {{L}_{1}}\times {{L}_{2}}=\overset{\wedge }{\mathop{i}}\,\left( 6 \right)-\overset{\wedge }{\mathop{j}}\,\left( -6 \right)+\overset{\wedge }{\mathop{k}}\,\left( -3 \right) \\\ & \Rightarrow {{L}_{1}}\times {{L}_{2}}=6\overset{\wedge }{\mathop{i}}\,+6\overset{\wedge }{\mathop{j}}\,-3\overset{\wedge }{\mathop{k}}\, \\\ \end{aligned}
Now, taking 3 as common from the above we get,
L1×L2=3(2i∧ +2j∧ −k∧ ){{L}_{1}}\times {{L}_{2}}=3\left( 2\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\, \right)
Hence, the direction ratios of the line L3{{L}_{3}} are equal to the coefficients of i∧ ,j∧ ,k∧ \overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,,\overset{\wedge }{\mathop{k}}\, which is:
(2,2,−1)\left( 2,2,-1 \right)
As you can see, the direction ratios of the two lines L1&L2{{L}_{1}}\And {{L}_{2}} are not the same so these two lines are not parallel to each other.
Now, if the two lines will meet each other then:
r1→=r2→\overrightarrow{{{r}_{1}}}=\overrightarrow{{{r}_{2}}} for some values of λ&μ\lambda \And \mu
i∧ +λ(−i∧ +2j∧ +2k∧ )=μ(2i∧ −j∧ +2k∧ ) ⇒i∧ (1−λ)+2λj∧ +2λk∧ =2μi∧ −μj∧ +2μk∧  \begin{aligned} & \overset{\wedge }{\mathop{i}}\,+\lambda \left( -\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+2\overset{\wedge }{\mathop{k}}\, \right)=\mu \left( 2\overset{\wedge }{\mathop{i}}\,-\overset{\wedge }{\mathop{j}}\,+2\overset{\wedge }{\mathop{k}}\, \right) \\\ & \Rightarrow \overset{\wedge }{\mathop{i}}\,\left( 1-\lambda \right)+2\lambda \overset{\wedge }{\mathop{j}}\,+2\lambda \overset{\wedge }{\mathop{k}}\,=2\mu \overset{\wedge }{\mathop{i}}\,-\mu \overset{\wedge }{\mathop{j}}\,+2\mu \overset{\wedge }{\mathop{k}}\, \\\ \end{aligned}
Now, equating i∧ ,j∧ ,k∧ \overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,,\overset{\wedge }{\mathop{k}}\, on both the sides we get,
1−λ=2μ, 2λ=−μ, 2λ=2μ \begin{aligned} & 1-\lambda =2\mu , \\\ & 2\lambda =-\mu , \\\ & 2\lambda =2\mu \\\ \end{aligned}
Solving the above equations, we get,
λ=μ, λ=−12μ \begin{aligned} & \lambda =\mu , \\\ & \lambda =-\dfrac{1}{2}\mu \\\ \end{aligned}
As you can see that we have two different types of λ\lambda are getting so r1→≠r2→\overrightarrow{{{r}_{1}}}\ne \overrightarrow{{{r}_{2}}} so these two lines won’t meet at some point.
Hence, the two lines L1&L2{{L}_{1}}\And {{L}_{2}} are not parallel and not intersecting with respect to each other so the two lines are skew.
In the below diagram, we have drawn two lines L1&L2{{L}_{1}}\And {{L}_{2}} and the line L3{{L}_{3}} which is perpendicular to both the lines

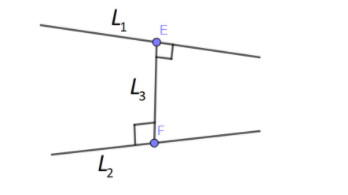
Let us assume two points each on lines L1&L2{{L}_{1}}\And {{L}_{2}} as point E and F with coordinates:
E(−λ+1,2λ,2λ), F(2μ,−μ,2μ) \begin{aligned} & E\left( -\lambda +1,2\lambda ,2\lambda \right), \\\ & F\left( 2\mu ,-\mu ,2\mu \right) \\\ \end{aligned}
Now, EF is perpendicular to both lines L1&L2{{L}_{1}}\And {{L}_{2}} so EF lies on the line L3{{L}_{3}} so the direction ratios of EF are equal to:
(2μ+λ−1,−μ−2λ,2μ−2λ)\left( 2\mu +\lambda -1,-\mu -2\lambda ,2\mu -2\lambda \right)
As we have already calculated the direction ratios for line L3{{L}_{3}} as (2,2,−1)\left( 2,2,-1 \right) so these direction ratios and the one that we have calculated above are proportional to each other.
2μ+λ−12=−μ−2λ2=2μ−2λ−1\dfrac{2\mu +\lambda -1}{2}=\dfrac{-\mu -2\lambda }{2}=\dfrac{2\mu -2\lambda }{-1}
Solving the above equations, by taking first and seconds fraction and first and third fraction we get,
2μ+λ−12=−μ−2λ2 ⇒2μ+λ−1=−μ−2λ ⇒3μ+3λ=1...........Eq.(1) \begin{aligned} & \dfrac{2\mu +\lambda -1}{2}=\dfrac{-\mu -2\lambda }{2} \\\ & \Rightarrow 2\mu +\lambda -1=-\mu -2\lambda \\\ & \Rightarrow 3\mu +3\lambda =1...........Eq.(1) \\\ \end{aligned}
2μ+λ−12=2μ−2λ−1 ⇒−2μ−λ+1=4μ−4λ ⇒6μ−3λ=1.........Eq.(2) \begin{aligned} & \dfrac{2\mu +\lambda -1}{2}=\dfrac{2\mu -2\lambda }{-1} \\\ & \Rightarrow -2\mu -\lambda +1=4\mu -4\lambda \\\ & \Rightarrow 6\mu -3\lambda =1.........Eq.(2) \\\ \end{aligned}
Adding eq. (1) and eq. (2) we get,
9μ=2 ⇒μ=29 \begin{aligned} & 9\mu =2 \\\ & \Rightarrow \mu =\dfrac{2}{9} \\\ \end{aligned}
Substituting the above value of μ\mu in eq. (1) we get,

& 3\left( \dfrac{2}{9} \right)+3\lambda =1 \\\ & \Rightarrow 3\lambda =1-\dfrac{6}{9} \\\ & \Rightarrow 3\lambda =1-\dfrac{2}{3} \\\ \end{aligned}$$ $$\begin{aligned} & \Rightarrow 3\lambda =\dfrac{1}{3} \\\ & \Rightarrow \lambda =\dfrac{1}{9} \\\ \end{aligned}$$ Hence, we got the value of $\lambda \And \mu $ as $\left( \dfrac{1}{9},\dfrac{2}{9} \right)$. Substituting the above values in E and F we get, $\begin{aligned} & E\left( -\dfrac{1}{9}+1,2\left( \dfrac{1}{9} \right),2\left( \dfrac{1}{9} \right) \right) \\\ & =E\left( \dfrac{8}{9},\left( \dfrac{2}{9} \right),\left( \dfrac{2}{9} \right) \right) \\\ & F\left( 2\left( \dfrac{2}{9} \right),-\left( \dfrac{2}{9} \right),2\left( \dfrac{2}{9} \right) \right) \\\ & =F\left( \left( \dfrac{4}{9} \right),-\left( \dfrac{2}{9} \right),\left( \dfrac{4}{9} \right) \right) \\\ \end{aligned}$ Now, take the midpoint of E and F by adding the coordinates of E and F and then dividing them by 2. $\begin{aligned} & \left( \dfrac{8}{9}+\dfrac{4}{9},\dfrac{2}{9}-\dfrac{2}{9},\dfrac{2}{9}+\dfrac{4}{9} \right) \\\ & =\left( \dfrac{12}{9},0,\dfrac{6}{9} \right) \\\ & =\left( \dfrac{4}{3},0,\dfrac{2}{3} \right) \\\ \end{aligned}$ Now, the equation of line ${{L}_{3}}$ is equal to: $\overrightarrow{r}=\overrightarrow{a}+t\left( 2\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\, \right)$ Now, $\overrightarrow{a}$ can be any of E, F and the midpoint of E and F. By substituting the point E in the above line ${{L}_{3}}$ equation we get, $\overrightarrow{r}=\dfrac{2}{9}\left( 4\overset{\wedge }{\mathop{i}}\,+\overset{\wedge }{\mathop{j}}\,+\overset{\wedge }{\mathop{k}}\, \right)+t\left( 2\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\, \right),t\in R$ By substituting the point F in the above line ${{L}_{3}}$ equation we get, $\overrightarrow{r}=\dfrac{2}{9}\left( 2\overset{\wedge }{\mathop{i}}\,-\overset{\wedge }{\mathop{j}}\,+2\overset{\wedge }{\mathop{k}}\, \right)+t\left( 2\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\, \right),t\in R$ By substituting the midpoint we get, $\overrightarrow{r}=\dfrac{1}{3}\left( 2\overset{\wedge }{\mathop{i}}\,+\overset{\wedge }{\mathop{k}}\, \right)+t\left( 2\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,-\overset{\wedge }{\mathop{k}}\, \right),t\in R$ Hence, the correct options are (a), (b) and (c). **Note** : You can extract the concepts that you used in this problem and can use in other questions like if we have two lines and third line is perpendicular to both of these lines then how can we find the direction ratios of the third line and also how to know whether the two lines are parallel, intersecting or skew.