Question
Question: Let $I(x) = \int \frac{dx}{(x-11)^{\frac{11}{13}}(x+15)^{\frac{15}{13}}}$. If $I(37) - I(24) = \fra...
Let I(x)=∫(x−11)1311(x+15)1315dx. If
I(37)−I(24)=41(b1311−c1311), b,c∈N, then 3(b+c) is equal to
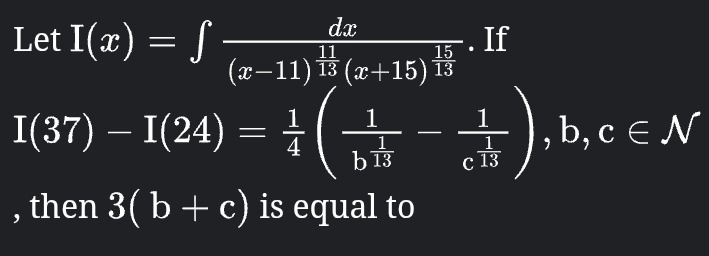
39
Solution
To evaluate the integral I(x)=∫(x−11)1311(x+15)1315dx, we first observe the powers in the denominator. The sum of the powers is 1311+1315=1326=2. This suggests a substitution of the form u=x−bx−a.
Let's rewrite the integrand by factoring out (x+15)2 from the denominator: I(x)=∫(x−11)1311(x+15)1311(x+15)134dx=∫((x−11)(x+15))1311(x+15)134dx This is not the most straightforward way. Instead, let's divide the numerator and denominator by (x+15)2: I(x)=∫(x+15)2(x−11)1311(x+15)1315(x+15)21dx=∫(x+15x−11)1311(x+15)21dx
Now, let u=x+15x−11. Differentiating u with respect to x: du=dxd(x+15x−11)dx=(x+15)2(x+15)(1)−(x−11)(1)dx du=(x+15)2x+15−x+11dx=(x+15)226dx From this, we have (x+15)2dx=261du.
Substitute u and du into the integral: I(x)=∫u13111⋅261du=261∫u−1311du Now, integrate u−1311: ∫u−1311du=−1311+1u−1311+1+C=132u132+C=213u132+C Substitute this back into the expression for I(x): I(x)=261⋅213u132+C=41u132+C Finally, substitute back u=x+15x−11: I(x)=41(x+15x−11)132+C
Now we need to evaluate I(37)−I(24). For definite integrals, the constant C cancels out. I(37)=41(37+1537−11)132=41(5226)132=41(21)132 I(24)=41(24+1524−11)132=41(3913)132=41(31)132 Subtracting I(24) from I(37): I(37)−I(24)=41[(21)132−(31)132] I(37)−I(24)=41[21321−31321] We can rewrite the terms in the form k131: 2132=(22)131=4131 3132=(32)131=9131 So, I(37)−I(24)=41[41311−91311] The problem states that I(37)−I(24)=41(b1311−c1311). Comparing the two expressions, we get b=4 and c=9. Both b and c are natural numbers, as required.
Finally, we need to find the value of 3(b+c): 3(b+c)=3(4+9)=3(13)=39
The final answer is 39.
Explanation of the solution:
- Identify the integral type: The integral is of the form ∫(x−a)m(x−b)ndx where m+n is an integer (11/13+15/13=2). This suggests a substitution u=x−bx−a.
- Choose substitution: Let u=x+15x−11.
- Calculate du: Find the derivative of u with respect to x, which is du=(x+15)226dx.
- Rewrite integrand: Express the original integrand in terms of u and du. This involves dividing the numerator and denominator by (x+15)2.
- Integrate: The integral transforms into 261∫u−1311du, which evaluates to 41u132.
- Substitute back: Replace u with x+15x−11 to get I(x)=41(x+15x−11)132.
- Evaluate definite integral: Calculate I(37) and I(24) and find their difference.
- Compare and solve: Match the result with the given form 41(b1311−c1311) to find b=4 and c=9.
- Calculate final expression: Compute 3(b+c).
The final answer is 39.
