Question

Let $\int_{0}^{a} \frac{cot^{-1}(e^x)+cot^{-1}(e^{-x})}{tan^{-1}a+tan^{-1}x} \cdot \frac{dx}{x^2+1} = \frac{\pi}{p} \ln q$, (a > 0) where p, q $\in$ N, then find the minimum value of (p+q)_____

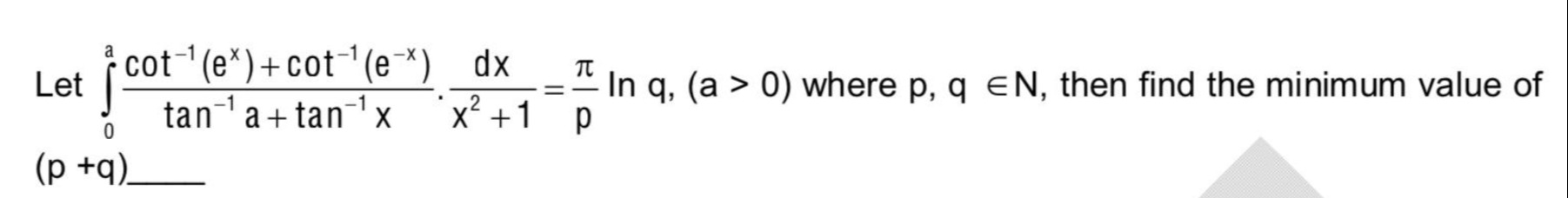
Answer 1

4

Answer 2

Solution Explanation

1. Simplify the Numerator:
   Note that

   $$\cot^{-1}(e^x)=\tan^{-1}(e^{-x}),\quad \cot^{-1}(e^{-x})=\tan^{-1}(e^{x})$$

   Hence,

   $$\cot^{-1}(e^x)+\cot^{-1}(e^{-x})=\tan^{-1}(e^x)+\tan^{-1}(e^{-x})=\frac{\pi}{2} \quad \text{(since } \tan^{-1}(u)+\tan^{-1}(1/u)=\frac{\pi}{2}\text{ for } u>0\text{)}.$$

2. Rewrite the Integral:
   The integral becomes

   $$I=\frac{\pi}{2}\int_0^a \frac{1}{\tan^{-1}(a)+\tan^{-1}(x)}\frac{dx}{1+x^2}.$$

3. Substitution:
   Set

   $$u=\tan^{-1}(x),\quad du=\frac{dx}{1+x^2}.$$

   When $x=0$, $u=0$; when $x=a$, $u=\tan^{-1}(a)$.
   Thus,

   $$I=\frac{\pi}{2}\int_0^{\tan^{-1}(a)} \frac{du}{\tan^{-1}(a)+u}.$$

4. Evaluate the Integral:
   The integral

   $$\int \frac{du}{A+u}=\ln|A+u| + C,\quad \text{where } A=\tan^{-1}(a).$$

   Compute:

   $$\int_0^{\tan^{-1}(a)} \frac{du}{\tan^{-1}(a)+u} = \ln\Bigl(\tan^{-1}(a)+\tan^{-1}(a)\Bigr)-\ln\Bigl(\tan^{-1}(a)\Bigr) =\ln\frac{2\,\tan^{-1}(a)}{\tan^{-1}(a)}=\ln 2.$$

   Therefore,

   $$I=\frac{\pi}{2}\ln2.$$

5. Compare with Given Form:
   The expression is given as

   $$I=\frac{\pi}{p}\ln q.$$

   Equate:

   $$\frac{\pi}{p}\ln q=\frac{\pi}{2}\ln2 \quad \Longrightarrow \quad p=2\quad \text{and}\quad q=2.$$

   Hence,

   $$p+q=2+2=4.$$

---

Answer

4

---

Subject, Chapter, and Topic

• Subject: Mathematics
• Chapter: Integration (especially Inverse Trigonometric Functions)
• Topic: Integration using substitution and inverse trigonometric identities

---

Difficulty Level: Easy

Question Type: integer