Solveeit Logo
Login

Question

Question: Let \(\mathbf { a } , \mathbf { b }\) and <img src="https://cdn.pureessence.tech/canvas_119.png?top_...

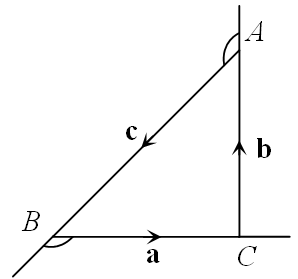
Let a,b\mathbf { a } , \mathbf { b } and be vectors with magnitudes 3, 4 and 5 respectively and a+b+c\mathbf { a } + \mathbf { b } + \mathbf { c } = 0, then the values of a⋅b+b⋅c+c⋅a\mathbf { a } \cdot \mathbf { b } + \mathbf { b } \cdot \mathbf { c } + \mathbf { c } \cdot \mathbf { a } is

A

47

B

25

C

50

D

– 25

Answer

– 25

Explanation

Solution

We observe,

∴\therefore a⋅b=0\mathbf { a } \cdot \mathbf { b } = 0

= −16- 16

= 5⋅3⋅{−cos⁡(cos⁡−135)}=5⋅3⋅(−35)5 \cdot 3 \cdot \left\{ - \cos \left( \cos ^ { - 1 } \frac { 3 } { 5 } \right) \right\} = 5 \cdot 3 \cdot \left( - \frac { 3 } { 5 } \right) = – 9

∴\therefore a⋅b+b⋅c+c⋅a=0−16−9=−25\mathbf { a } \cdot \mathbf { b } + \mathbf { b } \cdot \mathbf { c } + \mathbf { c } \cdot \mathbf { a } = 0 - 16 - 9 = - 25 Trick: ∙∙\bullet \bullet a+b+c=0\mathbf { a } + \mathbf { b } + \mathbf { c } = \mathbf { 0 }

Squaring both the sides ∣a+b+c∣2=0| \mathbf { a } + \mathbf { b } + \mathbf { c } | ^ { 2 } = 0

⇒∣a2∣+∣b∣2+∣c∣2+2(a⋅b+b⋅c+c⋅a)=0\left| \mathbf { a } ^ { 2 } \right| + | \mathbf { b } | ^ { 2 } + | \mathbf { c } | ^ { 2 } + 2 ( \mathbf { a } \cdot \mathbf { b } + \mathbf { b } \cdot \mathbf { c } + \mathbf { c } \cdot \mathbf { a } ) = 0

⇒

⇒ a⋅b+b⋅c+c⋅a=−25\mathbf { a } \cdot \mathbf { b } + \mathbf { b } \cdot \mathbf { c } + \mathbf { c } \cdot \mathbf { a } = - 25