Question

Let image of point $A\left( 3,1 \right)$ about line $x+y+7=0$ be $B\left( \alpha ,\beta \right)$ and image of $B\left( \alpha ,\beta \right)$ about line $x-2y+4=0$ be $C\left( \gamma ,8 \right)$ , then the circumcentre of $\Delta ABC$ is
A. $\left( -8,2 \right)$
B. $\left( -8,-1 \right)$
C. $\left( -6,-1 \right)$
D. $\left( -8,0 \right)$

Answer 1

Hint : We first try to find the points and their actual values. The lines will be perpendicular and the points will have their midpoint on the line. We use these tricks to find the equations. We solve them to find the solution.

Complete step by step solution:
Let image of point $A\left( 3,1 \right)$ about line $x+y+7=0$ be $B\left( \alpha ,\beta \right)$ and image of $B\left( \alpha ,\beta \right)$ about line $x-2y+4=0$ be $C\left( \gamma ,8 \right)$ .
We know that any point and its image point are at the same distance from the mirror line.
The mid-point of them will be on the line.
The mid-point of $A\left( 3,1 \right)$ and $B\left( \alpha ,\beta \right)$ is $M\equiv \left( \dfrac{3+\alpha }{2},\dfrac{1+\beta }{2} \right)$ .
M lies on the line $x+y+7=0$ which means the coordinates satisfy the equation.
Therefore, $\dfrac{3+\alpha }{2}+\dfrac{1+\beta }{2}+7=0$ .
Simplifying we get
$\begin{aligned} & \dfrac{3+\alpha }{2}+\dfrac{1+\beta }{2}+7=0 \\\ & \Rightarrow 18+\alpha +\beta =0 \\\ \end{aligned}$
These lines are also perpendicular to each other. $A\left( 3,1 \right)$ is on the perpendicular of $x+y+7=0$ .
Therefore, the slopes are $-1$ and $\dfrac{\beta -1}{\alpha -3}$ which gives $\dfrac{\beta -1}{\alpha -3}\times \left( -1 \right)=-1$ . So, $\beta -1=\alpha -3$ .
Solving them we get $\alpha =-8;\beta =-10$ .
Similarly, the mid-point of $B\left( -8,-10 \right)$ and $C\left( \gamma ,8 \right)$ is $N\equiv \left( \dfrac{-8+\gamma }{2},\dfrac{-10+8}{2} \right)\equiv \left( \dfrac{-8+\gamma }{2},-1 \right)$ .
N lies on the line $x-2y+4=0$ which means the coordinates satisfy the equation.
Therefore, $\dfrac{-8+\gamma }{2}+2+4=0$ .
Simplifying we get
$\begin{aligned} & \dfrac{-8+\gamma }{2}+2+4=0 \\\ & \Rightarrow \gamma =-4 \\\ \end{aligned}$
The points are $A\left( 3,1 \right)$ , $B\left( -8,-10 \right)$ , $C\left( -4,8 \right)$ .
If the circumcentre is $X\left( h,k \right)$ , then ${{\left( h-3 \right)}^{2}}+{{\left( k-1 \right)}^{2}}={{\left( h+8 \right)}^{2}}+{{\left( k+10 \right)}^{2}}$.
Simplifying we get
$\begin{aligned} & -6h+9-2k+1=16h+64+20k+100 \\\ & \Rightarrow h+k=-7 \\\ \end{aligned}$
Also ${{\left( h+4 \right)}^{2}}+{{\left( k-8 \right)}^{2}}={{\left( h+8 \right)}^{2}}+{{\left( k+10 \right)}^{2}}$.
Simplifying we get
$\begin{aligned} & 8h+16-16k+64=16h+64+20k+100 \\\ & \Rightarrow 2h+9k=-21 \\\ \end{aligned}$
The solution of the two equations is $h=-6,k=-1$ . The correct option is C.

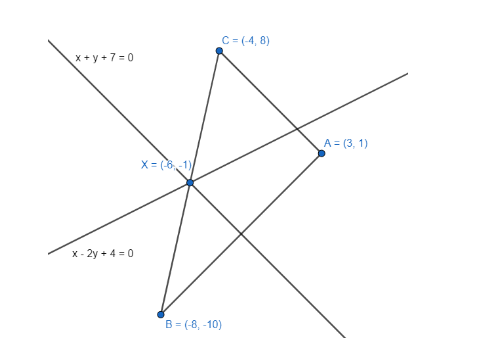
So, the correct answer is “Option C”.

Note : The distance of the midpoint of the sides from the circumcentre is equal for all three parts. We use that to find the coordinates of the point.