Question

Let $I=\int_{\dfrac{\pi }{4}}^{\dfrac{\pi }{3}}{\dfrac{\sin x}{x}dx}$, then
[a] $\dfrac{1}{2}\le I\le 1$
[b] $4\le I\le 2\sqrt{30}$
[c] $\dfrac{\sqrt{3}}{8}\le I\le \dfrac{\sqrt{2}}{6}$
[d] $1\le I\le \dfrac{2\sqrt{3}}{\sqrt{2}}$

Answer 1

Hint: Use the fact that $\dfrac{\sin x}{x}$ is decreasing function in the interval $\left( \dfrac{\pi }{4},\dfrac{\pi }{3} \right)$.
Use the fact that if f(x) is a decreasing function in (a,b), then $f\left( b \right)\left( b-a \right)\le \int_{a}^{b}{f\left( x \right)dx\le f\left( a \right)\left( b-a \right)}$.
Hence find the corresponding range of $\int_{\dfrac{\pi }{4}}^{\dfrac{\pi }{3}}{\dfrac{\sin x}{x}dx}$.

Complete step-by-step answer:

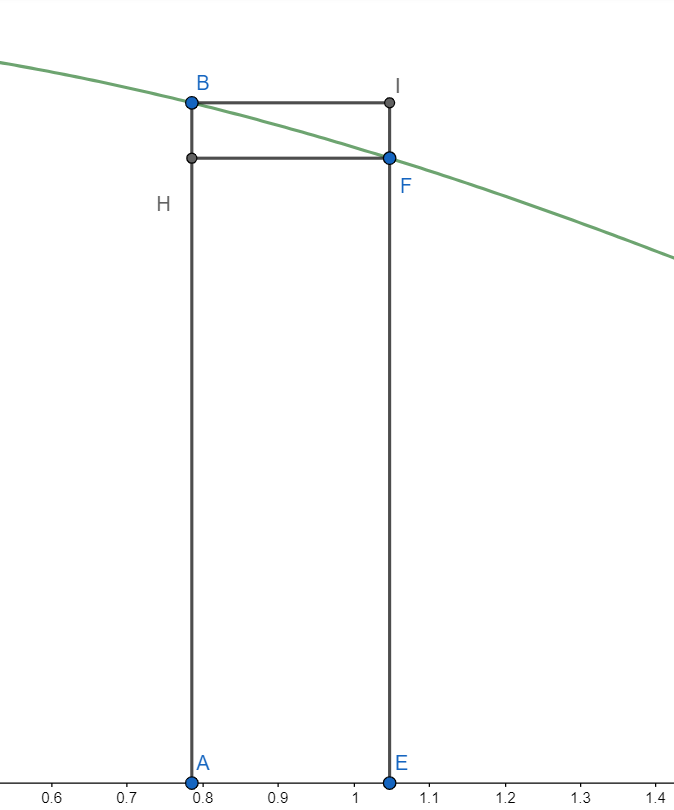
The green curve is of $\dfrac{\sin x}{x}$, $A\equiv \left( \dfrac{\pi }{4},0 \right)$ and $E\equiv \left( \dfrac{\pi }{3},0 \right)$.
As is evident from the graph, the area of rectangle BIEA is more than the value of the integral, and the area of the rectangle HFEA is less than the value of the integral.
Now we have
Area of rectangle BIEA $=AE\times AB=\dfrac{\sin \left( \dfrac{\pi }{4} \right)}{\dfrac{\pi }{4}}\left( \dfrac{\pi }{3}-\dfrac{\pi }{4} \right)$
Now, we know that $\sin \left( \dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}$
Using, we get
Area of rectangle BIEA $=\dfrac{\dfrac{1}{\sqrt{2}}}{\pi }\times 4\times \left( \dfrac{4\pi -3\pi }{12} \right)=\dfrac{1}{3\sqrt{2}}$
Multiplying the numerator and denominator by $\sqrt{2}$, we get
Area of rectangle BIEA $=\dfrac{\sqrt{2}}{6}$.
Also, the area of rectangle HFEA $=AH\times AE=\dfrac{\sin \left( \dfrac{\pi }{3} \right)}{\dfrac{\pi }{3}}\times \left( \dfrac{\pi }{3}-\dfrac{\pi }{4} \right)$
We know that $\sin \left( \dfrac{\pi }{3} \right)=\dfrac{\sqrt{3}}{2}$
Using, we get
Area of rectangle HFEA $=\dfrac{\dfrac{\sqrt{3}}{2}}{\pi }\times 3\times \dfrac{\pi }{12}=\dfrac{\sqrt{3}}{8}$
Now we know that the area of rectangle BIEA is more than the value of the integral and the area of the rectangle HFEA is less than the value of the integral.
Hence we have
$\dfrac{\sqrt{3}}{8}\le I\le \dfrac{\sqrt{2}}{6}$
Hence option [c] is correct

Note: If M is the maxima of f(x) and m is the minima of f(x) in the interval (a,b), the we have $m\left( b-a \right)\le \int_{a}^{b}{f\left( x \right)dx}\le M\left( b-a \right)$
Now let f(x) $=\dfrac{\sin x}{x}$, we have
$\begin{aligned} & f'\left( x \right)=\dfrac{x\cos x-\sin x}{{{x}^{2}}} \\\ & \Rightarrow f'\left( x \right)=\cos x\dfrac{x-\tan x}{{{x}^{2}}} \\\ \end{aligned}$
Now, we know that $\tan x\ge x,x\in \left( 0,\dfrac{\pi }{2} \right)$ and in the interval $\left( \dfrac{\pi }{4},\dfrac{\pi }{3} \right),x>0,\cos x<1$. Hence, we have
$\cos x\dfrac{x-\tan x}{{{x}^{2}}}\le 0$
Hence we have
$f'\left( x \right)\le 0$
Hence f(x) is a decreasing function in the interval $\left( \dfrac{\pi }{4},\dfrac{\pi }{3} \right)$.
Hence we have
$\forall {{x}_{1}},{{x}_{2}}\in \left( \dfrac{\pi }{4},\dfrac{\pi }{3} \right)$ if ${{x}_{1}}<{{x}_{2}}$, then $f\left( {{x}_{1}} \right)\ge f\left( {{x}_{2}} \right)$.
Hence we have $m=\dfrac{\sin \left( \dfrac{\pi }{3} \right)}{\dfrac{\pi }{3}}=\dfrac{3\sqrt{3}}{2\pi }$ and $M=\dfrac{\sin \left( \dfrac{\pi }{4} \right)}{\dfrac{\pi }{4}}=\dfrac{4\sqrt{2}}{2\pi }$
Hence we have
$\begin{aligned} & \dfrac{3\sqrt{3}}{2\pi }\left( \dfrac{\pi }{12} \right)\le I\le \dfrac{4\sqrt{2}}{2\pi }\left( \dfrac{\pi }{12} \right) \\\ & \Rightarrow \dfrac{\sqrt{3}}{8}\le I\le \dfrac{\sqrt{2}}{6} \\\ \end{aligned}$
Hence option [c] is correct.
[2] Inequality $\tan x\ge x,x\in \left( 0,\dfrac{\pi }{2} \right)$ follows from LMVT
Apply LMVT in $\left[ 0.x \right]$ where $x\in \left( 0,\dfrac{\pi }{2} \right)$, we have $\dfrac{\tan x}{x-0}={{\sec }^{2}}c,c\in \left( 0,x \right)$.
Now, we know ${{\sec }^{2}}x\ge 1$
Hence, we have
$\tan x\ge x$