Question

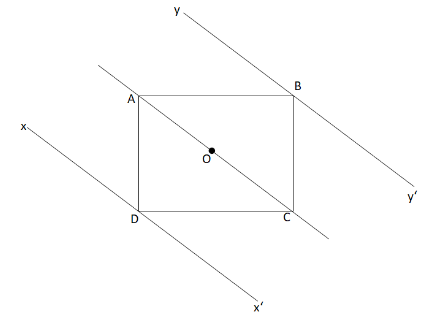
Let ${I_1}$, ${I_2}$ and ${I_3}$ be the moment of inertia of a uniform square plate about axes AOC, $xDx'$ and $yBy'$ respectively as shown in the figure. The moments of inertia of the plate ${I_1}:{I_2}:{I_3}$ are in the ratio.

A. $1:\dfrac{1}{7}:\dfrac{1}{7}$
B. $1:\dfrac{{12}}{7}:\dfrac{{12}}{7}$
C. $1:\dfrac{7}{{12}}:\dfrac{7}{{12}}$
D. $1:7:7$

Answer 1

We are asked to find the ratios of the moments of inertia of the square plate about the given axes. Recall the formula to find the moment of inertia of a square along its diagonal for axis AOC. For the other two axis you will need to use parallel axis theorem, using this theorem find the moment of inertia about the other two axes. And find the required ratio.

Complete step by step answer:
Given a uniform square plate,moment of inertia about axis AOC is ${I_1}$.Moment of inertia about axis $xDx'$ is ${I_2}$.Moment of inertia about axis $yBy'$ is ${I_3}$.Let $m$ be the mass of the square plate and $l$ be the length of sides of the square plate.
The moment of inertia of a square about its diagonal is given by,
$I = \dfrac{{m{l^2}}}{{12}}$ ………………(i)
Here, the axis AOC is diagonal of the square plate, so moment of inertia about AOC can be written using the formula from equation (i), that is,
${I_1} = \dfrac{{m{l^2}}}{{12}}$ ……………………(ii)
The axes $xDx'$ and $yBy'$ are in symmetry, so moment of inertia of both axes will be same, that is
${I_2} = {I_3}$ ………………....(iii)

Now, we will find the moment of inertia about the axis $xDx'$ that is we will find ${I_2}$
We observe that the axis $xDx'$ is parallel to the axis AOC. Therefore we will use here parallel axis theorem. According to parallel axis theorem, the moment of inertia of a body about an axis which is parallel to an axis passing through its centre is the sum of the moment of inertia about the axis passing through its centre and product of the mass of the body and square of the distance between the two axes. That is,
$I = {I_{centre}} + m{d^2}$ ………………………(iv)
where ${I_{centre}}$ is the moment of inertia about an axis passing through the centre of the body and $d$ is the distance between the two axes.
Here,
${I_{centre}} = {I_1} = \dfrac{{m{l^2}}}{{12}}$ ………………………(v)
Now, we will find the distance between the axes AOC and $xDx'$ which is OD
We know the length of the diagonal of a square is given as,
$D = \sqrt 2 a$ where $a$ is the side of the square,
So, the length of the diagonal BD will be,
${\text{BD}} = \sqrt 2 l$

The axis passes through the centre of the square plate so, it will divide the line BD into two equal parts, that is
${\text{OD}} = \dfrac{1}{2}{\text{BD}}$
Putting the value of BD we get,
${\text{OD}} = \dfrac{1}{2}\sqrt 2 l = \dfrac{l}{{\sqrt 2 }}$
Now, moment of inertia about the axis $xDx'$ using the formula of parallel axis theorem from equation (iv), we get
${I_2} = {I_1} + m{({\text{OD}})^2}$
Putting the values of ${I_1}$ and ${\text{OD}}$, we get
${I_2} = \dfrac{{m{l^2}}}{{12}} + m{\left( {\dfrac{l}{{\sqrt 2 }}} \right)^2}$
$\Rightarrow {I_2} = \dfrac{{m{l^2}}}{{12}} + {\dfrac{{ml}}{2}^2}$
$\Rightarrow {I_2} = {\dfrac{{7ml}}{{12}}^2}$ …………………………....(vi)
From equation (ii), (iii) and (vi), we get
${I_1} = \dfrac{{m{l^2}}}{{12}}$ and ${I_2} = {I_3} = {\dfrac{{7ml}}{{12}}^2}$
Now, the ratios of moments of inertia of the plate is,
${I_1}:{I_2}:{I_3} = \dfrac{{m{l^2}}}{{12}}:{\dfrac{{7ml}}{{12}}^2}:{\dfrac{{7ml}}{{12}}^2}\\\$
$\therefore {I_1}:{I_2}:{I_3} = 1:7:7$
Therefore, the ratios are ${I_1}:{I_2}:{I_3} = 1:7:7$

Hence, option D is the correct answer.

Note: Moment of inertia can be understood as the resistance or opposition exhibited by a body to its rotation about an axis. Remember, there are two important theorems which are useful in finding moments of inertia about an axis of a body, these are perpendicular axis theorem and parallel axis theorem. In the above question we have discussed the parallel axis theorem.