Question

Let $g: R \rightarrow \{4\}$ be function given by $g(x) = x^3(f'(t) - 2) + x^2 f''(t) + 4x(f(0) + 6) + 4$ and $h(x)$ is defined as:

$h(x) = \begin{cases} \int_{0}^{x} |f(t) - 2| dt, & 0 \leq x \leq 6 \\ (x - 6)^2 + 20, & 6 < x \leq 12 \end{cases}$

If number of integers in the range of $h(x)$ is $N$ then _______.

Answer 1

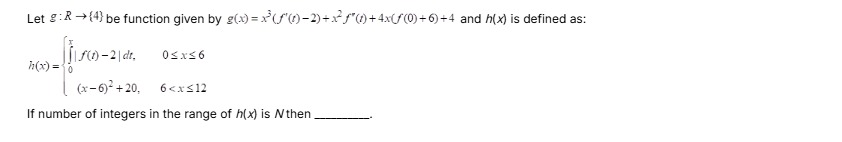
57

Answer 2

The condition $g: R \rightarrow \{4\}$ implies that $g(x)$ is a constant function equal to 4. For the given polynomial $g(x)$ to be constant, the coefficients of $x^3$, $x^2$, and $x$ must be zero. This leads to:

1. $f'(t) - 2 = 0 \implies f'(t) = 2$.
2. $f''(t) = 0$.
3. $f(0) + 6 = 0 \implies f(0) = -6$.

From $f'(t) = 2$ and $f''(t) = 0$, we deduce that $f(t)$ is a linear function of the form $f(t) = 2t + C$. Using the condition $f(0) = -6$, we find $2(0) + C = -6$, which gives $C = -6$. Therefore, $f(t) = 2t - 6$.

Now, we analyze $h(x)$:

Case 1: $0 \leq x \leq 6$ $h(x) = \int_{0}^{x} |f(t) - 2| dt = \int_{0}^{x} |(2t - 6) - 2| dt = \int_{0}^{x} |2t - 8| dt$. The expression $|2t - 8|$ changes sign at $t = 4$.

• For $0 \leq x \leq 4$: $|2t - 8| = -(2t - 8) = 8 - 2t$ since $2t - 8 \leq 0$ in $[0, x]$. $h(x) = \int_{0}^{x} (8 - 2t) dt = [8t - t^2]_{0}^{x} = 8x - x^2$. The range of $h(x) = 8x - x^2$ for $x \in [0, 4]$ is $[h(0), h(4)] = [0, 16]$.

• For $4 < x \leq 6$: We split the integral at $t=4$. $h(x) = \int_{0}^{4} (8 - 2t) dt + \int_{4}^{x} (2t - 8) dt$. $\int_{0}^{4} (8 - 2t) dt = [8t - t^2]_{0}^{4} = 32 - 16 = 16$. $\int_{4}^{x} (2t - 8) dt = [t^2 - 8t]_{4}^{x} = (x^2 - 8x) - (16 - 32) = x^2 - 8x + 16 = (x - 4)^2$. So, $h(x) = 16 + (x - 4)^2$. The range of $h(x) = 16 + (x - 4)^2$ for $x \in (4, 6]$ is $(16 + (4-4)^2, 16 + (6-4)^2] = (16, 16 + 4] = (16, 20]$.

Combining these two sub-cases for $0 \leq x \leq 6$, the range of $h(x)$ is $[0, 16] \cup (16, 20] = [0, 20]$.

Case 2: $6 < x \leq 12$ $h(x) = (x - 6)^2 + 20$. This is an increasing quadratic function for $x \in (6, 12]$. The range of $h(x)$ for $x \in (6, 12]$ is $((6-6)^2 + 20, (12-6)^2 + 20] = (0 + 20, 6^2 + 20] = (20, 36 + 20] = (20, 56]$.

Overall Range of $h(x)$: The domain of $h(x)$ is $[0, 12]$. The overall range is the union of the ranges from the two cases: $[0, 20] \cup (20, 56] = [0, 56]$.

Number of Integers in the Range: The range of $h(x)$ is $[0, 56]$. The integers in this range are $0, 1, 2, \dots, 56$. The number of integers, $N$, is $56 - 0 + 1 = 57$. The question asks for the value of $N$, which is 57.