Question

Let $f(x)=x^2+x\sin x - \cos x$. Then

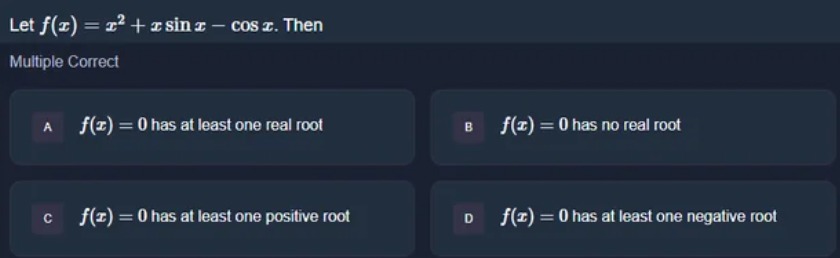
• A. $f(x)=0$ has at least one real root
• B. $f(x)=0$ has no real root
• C. $f(x)=0$ has at least one positive root
• D. $f(x)=0$ has at least one negative root

Answer 1

Answer: (A), (C), (D)

Options A, C, and D are correct.

Answer 2

Here's a breakdown of the solution:

1. Evaluation at 0:

   $f(0) = 0^2 + 0 \cdot \sin(0) - \cos(0) = -1$.

2. Behavior for large $x > 0$:

   As $x \to +\infty$, $x^2$ dominates, so $f(x) > 0$. By the Intermediate Value Theorem (IVT), since $f(0) = -1$ and $f(x) > 0$ for large $x$, there exists at least one positive root.

3. Symmetry of function:

   Notice that $f(-x) = (-x)^2 + (-x)\sin(-x) - \cos(-x) = x^2 + x\sin x - \cos x = f(x)$, so $f(x)$ is an even function. Thus, any positive root implies a corresponding negative root.

Conclusion:

• Option A: True, since there is at least one real root.
• Option B: False, since roots exist.
• Option C: True, as there is a positive root.
• Option D: True, as symmetry guarantees a negative root too.