Question
Question: Let $f(x)=\int \frac{1+(x \ln x)^2}{x \ln x}dx$ such that $f(e)=\frac{e^2}{4}$. Then the value of $4...
Let f(x)=∫xlnx1+(xlnx)2dx such that f(e)=4e2. Then the value of 4(e2f(e1)+1) is
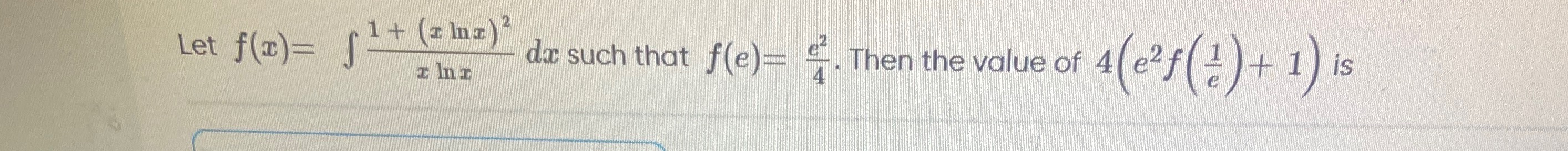
1
Solution
To find the value of 4(e2f(e1)+1), we first need to determine the function f(x) by evaluating the given integral and then use the initial condition to find the constant of integration.
The given integral is f(x)=∫xlnx1+(xlnx)2dx. We can split the integrand into two parts: f(x)=∫(xlnx1+xlnx(xlnx)2)dx f(x)=∫(xlnx1+xlnx)dx This can be written as the sum of two integrals: f(x)=∫xlnx1dx+∫xlnxdx
Let's evaluate the first integral, I1=∫xlnx1dx: Let u=lnx. Then, du=x1dx. Substituting these into the integral: I1=∫u1du=ln∣u∣+C1=ln∣lnx∣+C1.
Now, let's evaluate the second integral, I2=∫xlnxdx: We use integration by parts, which states ∫pdq=pq−∫qdp. Let p=lnx and dq=xdx. Then, dp=x1dx and q=2x2. Substituting these into the integration by parts formula: I2=(lnx)(2x2)−∫(2x2)(x1)dx I2=2x2lnx−∫2xdx I2=2x2lnx−4x2+C2.
Combining the results for I1 and I2, we get the function f(x): f(x)=ln∣lnx∣+2x2lnx−4x2+C, where C=C1+C2.
Next, we use the given condition f(e)=4e2 to find the value of C. Substitute x=e into the expression for f(x): f(e)=ln∣lne∣+2e2lne−4e2+C Since lne=1: f(e)=ln∣1∣+2e2(1)−4e2+C f(e)=0+2e2−4e2+C f(e)=42e2−e2+C f(e)=4e2+C. We are given that f(e)=4e2. Therefore: 4e2=4e2+C This implies C=0.
So, the function f(x) is: f(x)=ln∣lnx∣+2x2lnx−4x2.
Finally, we need to find the value of 4(e2f(e1)+1). First, let's evaluate f(e1): Substitute x=e1 into the expression for f(x): f(e1)=lnln(e1)+2(e1)2ln(e1)−4(e1)2 We know that ln(e1)=ln(e−1)=−1. So, f(e1)=ln∣−1∣+2e21(−1)−4e21 Since ln∣−1∣=ln(1)=0: f(e1)=0−2e21−4e21 f(e1)=−4e22−4e21 f(e1)=−4e23.
Now, substitute this value into the expression 4(e2f(e1)+1): 4(e2(−4e23)+1) =4(−43+1) =4(4−3+4) =4(41) =1.
The final answer is 1.
Explanation of the solution:
- Decompose the integral: The integrand xlnx1+(xlnx)2 is split into two simpler terms: xlnx1 and xlnx.
- Integrate each term:
- ∫xlnx1dx: Use substitution u=lnx, leading to ln∣lnx∣.
- ∫xlnxdx: Use integration by parts, leading to 2x2lnx−4x2.
- Combine and find constant: Sum the results of the two integrals to get f(x)=ln∣lnx∣+2x2lnx−4x2+C. Use the condition f(e)=4e2 to determine C=0.
- Evaluate at specific point: Calculate f(e1) by substituting x=e1 into the derived f(x), which gives −4e23.
- Final calculation: Substitute f(e1) into the expression 4(e2f(e1)+1) and simplify to get 1.
