Question
Question: Let $f(x)=1+2\cos x+3\sin x$. If real numbers a, b, c are such that $a f(x)+b f(c-x)=1$ holds for an...
Let f(x)=1+2cosx+3sinx. If real numbers a, b, c are such that af(x)+bf(c−x)=1 holds for any x∈R
then abcosc=
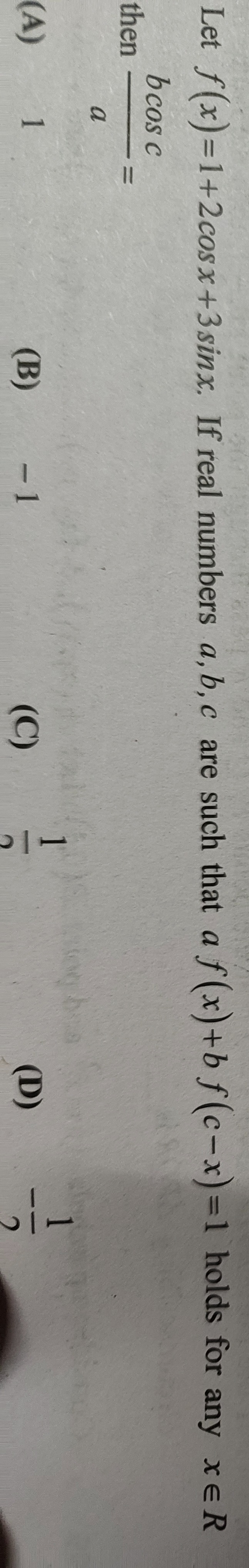
A
1
B
-1
C
31
D
−21
Answer
135
Explanation
Solution
We are given
f(x)=1+2cosx+3sinx,and
af(x)+bf(c−x)=1for all x∈R.Since the identity holds for all x, the coefficients of cosx and sinx must vanish and the constant term must match.
- Write
Using the cosine and sine angle‐difference formulas:
cos(c−x)=cosccosx+sincsinx, sin(c−x)=sinccosx−coscsinx,we obtain
f(c−x)=1+(2cosc+3sinc)cosx+(2sinc−3cosc)sinx.- Now,
Collect coefficients:
- Constant term: a+b
- Coefficient of cosx: 2a+b(2cosc+3sinc)
- Coefficient of sinx: 3a+b(2sinc−3cosc)
For the identity to be 1 (with no cosx or sinx terms) we must have:
a+b=1,2a+b(2cosc+3sinc)=0,3a+b(2sinc−3cosc)=0.- From the second equation:
Substitute this into the third equation:
3[−2b(2cosc+3sinc)]+b(2sinc−3cosc)=0.Multiply by 2:
−3b(2cosc+3sinc)+2b(2sinc−3cosc)=0.Factor b (noting b=0):
−3(2cosc+3sinc)+2(2sinc−3cosc)=0.Expanding:
−6cosc−9sinc+4sinc−6cosc=0⟹−12cosc−5sinc=0.Thus,
12cosc+5sinc=0⟹sinc=−512cosc.- Now substitute sinc=−512cosc back into the equation for a from step 3:
- We need the value of abcosc:
Thus the required ratio is 135.
