Question

Let $f(x) = x^4-2x^2 + 2$, $x \in (-\infty, \infty)$ and $g(x) =$

$$\operatorname{Lim}_{n \rightarrow \infty} \frac{(f(x))^n-1}{(f(x))^n+1}, \text{ then the value of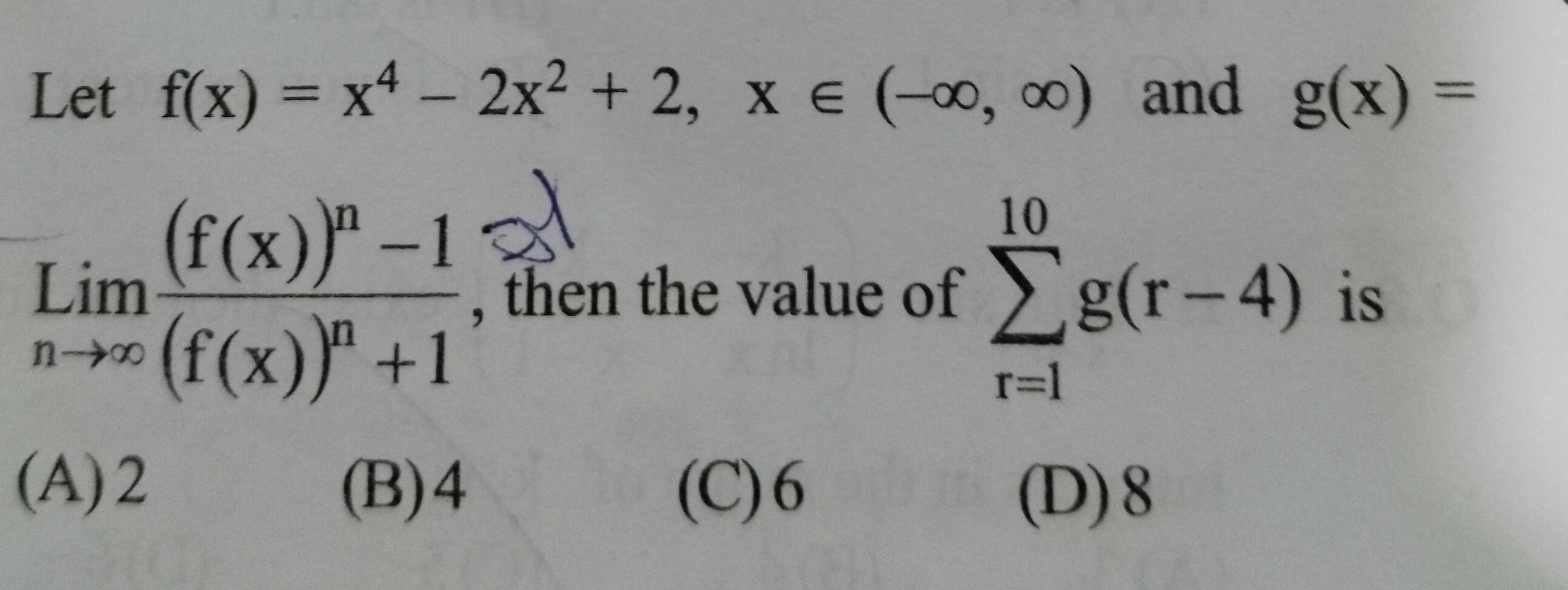 } \sum_{r=1}^{10} g(r-4) \text{ is}$$

• A. 2
• B. 4
• C. 6
• D. 8

Answer 1

Answer: (D)

8

Answer 2

Let $f(x) = x^4-2x^2 + 2$. We can rewrite $f(x)$ by completing the square:
$f(x) = (x^2)^2 - 2(x^2) + 1 + 1 = (x^2-1)^2 + 1$.
Since $(x^2-1)^2 \ge 0$ for all real $x$, the minimum value of $f(x)$ is $0+1=1$, which occurs when $x^2-1=0$, i.e., $x=\pm 1$.
For all other values of $x$, $(x^2-1)^2 > 0$, so $f(x) > 1$.
Thus, $f(x) \ge 1$ for all $x \in (-\infty, \infty)$.

Now consider the function $g(x) = \operatorname{Lim}_{n \rightarrow \infty} \frac{(f(x))^n-1}{(f(x))^n+1}$.
Let $y = f(x)$. We need to evaluate $\operatorname{Lim}_{n \rightarrow \infty} \frac{y^n-1}{y^n+1}$.

Case 1: $y > 1$. Divide the numerator and denominator by $y^n$:
$\operatorname{Lim}_{n \rightarrow \infty} \frac{y^n-1}{y^n+1} = \operatorname{Lim}_{n \rightarrow \infty} \frac{1-1/y^n}{1+1/y^n}$. Since $y > 1$, $\operatorname{Lim}_{n \rightarrow \infty} 1/y^n = 0$.
So, the limit is $\frac{1-0}{1+0} = 1$.

Case 2: $y = 1$.
$\operatorname{Lim}_{n \rightarrow \infty} \frac{1^n-1}{1^n+1} = \frac{1-1}{1+1} = \frac{0}{2} = 0$.

Since $f(x) \ge 1$ for all $x$, these are the only cases we need to consider for $y=f(x)$.
So, the function $g(x)$ is defined as:
$g(x) = 1$ if $f(x) > 1$
$g(x) = 0$ if $f(x) = 1$

We know that $f(x) = 1$ when $x=\pm 1$, and $f(x) > 1$ when $x \ne \pm 1$.
Therefore, the function $g(x)$ can be written as:
$g(x) = \begin{cases} 0 & \text{if } x = -1 \text{ or } x = 1 \\ 1 & \text{if } x \ne -1 \text{ and } x \ne 1 \end{cases}$

We need to find the value of the sum $\sum_{r=1}^{10} g(r-4)$.
The terms in the sum are $g(r-4)$ for $r=1, 2, \dots, 10$.
Let $k = r-4$. As $r$ goes from 1 to 10, $k$ goes from $1-4=-3$ to $10-4=6$.
The sum is $\sum_{k=-3}^{6} g(k)$.
The arguments of $g$ in the sum are the integers in the set $\{-3, -2, -1, 0, 1, 2, 3, 4, 5, 6\}$.

We need to evaluate $g(k)$ for each $k$ in this set:
$g(-3)$: $-3 \ne \pm 1$, so $g(-3)=1$.
$g(-2)$: $-2 \ne \pm 1$, so $g(-2)=1$.
$g(-1)$: $-1 = -1$, so $g(-1)=0$.
$g(0)$: $0 \ne \pm 1$, so $g(0)=1$.
$g(1)$: $1 = 1$, so $g(1)=0$.
$g(2)$: $2 \ne \pm 1$, so $g(2)=1$.
$g(3)$: $3 \ne \pm 1$, so $g(3)=1$.
$g(4)$: $4 \ne \pm 1$, so $g(4)=1$.
$g(5)$: $5 \ne \pm 1$, so $g(5)=1$.
$g(6)$: $6 \ne \pm 1$, so $g(6)=1$.

The sum is the sum of these values:
$\sum_{r=1}^{10} g(r-4) = g(-3) + g(-2) + g(-1) + g(0) + g(1) + g(2) + g(3) + g(4) + g(5) + g(6)$
$= 1 + 1 + 0 + 1 + 0 + 1 + 1 + 1 + 1 + 1$

There are 10 terms in total.
The terms where $g(k)=0$ are for $k=-1$ and $k=1$. There are 2 such terms.
The terms where $g(k)=1$ are for the remaining $10-2=8$ values of $k$.
The sum is $(8 \times 1) + (2 \times 0) = 8 + 0 = 8$.