Question

Let $f(x) = x^3 + 3x + 2$ and $g(x)$ is the inverse of it. Find the area bounded by $g(x)$, the x-axis and the ordinate at $x = -2$ and $x = 6$.

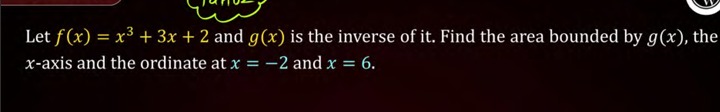
Answer 1

$\frac{9}{2}$

Answer 2

• The area is calculated by integrating the absolute value of the inverse function $g(x)$ from $x=-2$ to $x=6$.
• We determine $g(-2) = -1$, $g(6) = 1$, and $g(2) = 0$.
• The area is split into $\int_{-2}^{2} -g(x) dx + \int_{2}^{6} g(x) dx$.
• Using the property $\int_a^b g(x) dx = b g(b) - a g(a) - \int_{g(a)}^{g(b)} f(y) dy$:
  • $-\int_{-2}^{2} g(x) dx = -[2(0) - (-2)(-1) - \int_{-1}^{0} (y^3 + 3y + 2) dy] = -[-2 - (-\frac{1}{4})] = -2 - \frac{1}{4} = \frac{9}{4}$.
  • $\int_{2}^{6} g(x) dx = [6(1) - 2(0) - \int_{0}^{1} (y^3 + 3y + 2) dy] = [6 - (\frac{15}{4})] = \frac{9}{4}$.
• Total Area = $\frac{9}{4} + \frac{9}{4} = \frac{9}{2}$.