Solveeit Logo
Login

Question

Question: Let $f(x) = \tan^{-1}\sqrt{\frac{1+\sin x}{1-\sin x}}$ for $x \in (\frac{\pi}{2}, \pi)$, then $\left...

Let f(x)=tan⁡−11+sin⁡x1−sin⁡xf(x) = \tan^{-1}\sqrt{\frac{1+\sin x}{1-\sin x}} for x∈(π2,π)x \in (\frac{\pi}{2}, \pi), then ∣2f′(2π3)∣\left|\frac{2}{f'(\frac{2\pi}{3})}\right| is equal to

Answer

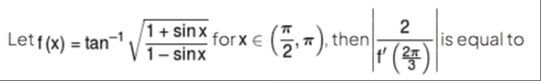
4

Explanation

Solution

The function is given by f(x)=tan⁡−11+sin⁡x1−sin⁡xf(x) = \tan^{-1}\sqrt{\frac{1+\sin x}{1-\sin x}} for x∈(π2,π)x \in (\frac{\pi}{2}, \pi).

First, we simplify the expression inside the square root. We use the identities 1+cos⁡θ=2cos⁡2(θ/2)1+\cos \theta = 2\cos^2(\theta/2) and 1−cos⁡θ=2sin⁡2(θ/2)1-\cos \theta = 2\sin^2(\theta/2). We can write sin⁡x=cos⁡(π2−x)\sin x = \cos(\frac{\pi}{2} - x). So, 1+sin⁡x1−sin⁡x=1+cos⁡(π2−x)1−cos⁡(π2−x)=2cos⁡2(π/2−x2)2sin⁡2(π/2−x2)=cos⁡2(π4−x2)sin⁡2(π4−x2)=cot⁡2(π4−x2)\frac{1+\sin x}{1-\sin x} = \frac{1+\cos(\frac{\pi}{2} - x)}{1-\cos(\frac{\pi}{2} - x)} = \frac{2\cos^2(\frac{\pi/2 - x}{2})}{2\sin^2(\frac{\pi/2 - x}{2})} = \frac{\cos^2(\frac{\pi}{4} - \frac{x}{2})}{\sin^2(\frac{\pi}{4} - \frac{x}{2})} = \cot^2(\frac{\pi}{4} - \frac{x}{2}).

Thus, 1+sin⁡x1−sin⁡x=cot⁡2(π4−x2)=∣cot⁡(π4−x2)∣\sqrt{\frac{1+\sin x}{1-\sin x}} = \sqrt{\cot^2(\frac{\pi}{4} - \frac{x}{2})} = \left|\cot(\frac{\pi}{4} - \frac{x}{2})\right|.

Now we need to determine the sign of cot⁡(π4−x2)\cot(\frac{\pi}{4} - \frac{x}{2}) for x∈(π2,π)x \in (\frac{\pi}{2}, \pi). If x∈(π2,π)x \in (\frac{\pi}{2}, \pi), then x2∈(π4,π2)\frac{x}{2} \in (\frac{\pi}{4}, \frac{\pi}{2}). So, π4−x2∈(π4−π2,π4−π4)=(−π4,0)\frac{\pi}{4} - \frac{x}{2} \in (\frac{\pi}{4} - \frac{\pi}{2}, \frac{\pi}{4} - \frac{\pi}{4}) = (-\frac{\pi}{4}, 0). In the interval (−π4,0)(-\frac{\pi}{4}, 0), the angle is in the fourth quadrant, where cosine is positive and sine is negative. Therefore, cot⁡\cot is negative. So, ∣cot⁡(π4−x2)∣=−cot⁡(π4−x2)\left|\cot(\frac{\pi}{4} - \frac{x}{2})\right| = -\cot(\frac{\pi}{4} - \frac{x}{2}).

Now, the function becomes f(x)=tan⁡−1(−cot⁡(π4−x2))f(x) = \tan^{-1}\left(-\cot(\frac{\pi}{4} - \frac{x}{2})\right). We use the identity −cot⁡θ=tan⁡(π2+θ)-\cot \theta = \tan(\frac{\pi}{2} + \theta). Let θ=π4−x2\theta = \frac{\pi}{4} - \frac{x}{2}. f(x)=tan⁡−1(tan⁡(π2+(π4−x2)))=tan⁡−1(tan⁡(3π4−x2))f(x) = \tan^{-1}\left(\tan(\frac{\pi}{2} + (\frac{\pi}{4} - \frac{x}{2}))\right) = \tan^{-1}\left(\tan(\frac{3\pi}{4} - \frac{x}{2})\right).

For tan⁡−1(tan⁡α)=α\tan^{-1}(\tan \alpha) = \alpha, the angle α\alpha must be in the principal range of tan⁡−1\tan^{-1}, which is (−π2,π2)(-\frac{\pi}{2}, \frac{\pi}{2}). Let's check the range of 3π4−x2\frac{3\pi}{4} - \frac{x}{2} for x∈(π2,π)x \in (\frac{\pi}{2}, \pi). Since x∈(π2,π)x \in (\frac{\pi}{2}, \pi), we have x2∈(π4,π2)\frac{x}{2} \in (\frac{\pi}{4}, \frac{\pi}{2}). Multiplying by -1 and reversing the inequality signs, we get −x2∈(−π2,−π4)-\frac{x}{2} \in (-\frac{\pi}{2}, -\frac{\pi}{4}). Adding 3π4\frac{3\pi}{4} to the interval, we get 3π4−x2∈(3π4−π2,3π4−π4)=(π4,π2)\frac{3\pi}{4} - \frac{x}{2} \in (\frac{3\pi}{4} - \frac{\pi}{2}, \frac{3\pi}{4} - \frac{\pi}{4}) = (\frac{\pi}{4}, \frac{\pi}{2}). The interval (π4,π2)(\frac{\pi}{4}, \frac{\pi}{2}) is within the principal range (−π2,π2)(-\frac{\pi}{2}, \frac{\pi}{2}). Therefore, f(x)=3π4−x2f(x) = \frac{3\pi}{4} - \frac{x}{2}.

Now we find the derivative f′(x)f'(x): f′(x)=ddx(3π4−x2)=0−12=−12f'(x) = \frac{d}{dx}(\frac{3\pi}{4} - \frac{x}{2}) = 0 - \frac{1}{2} = -\frac{1}{2}.

The derivative is a constant, so f′(2π3)=−12f'(\frac{2\pi}{3}) = -\frac{1}{2}.

We need to calculate ∣2f′(2π3)∣\left|\frac{2}{f'(\frac{2\pi}{3})}\right|. ∣2−12∣=∣2×(−2)∣=∣−4∣=4\left|\frac{2}{-\frac{1}{2}}\right| = \left|2 \times (-2)\right| = \left|-4\right| = 4.

The final answer is ∣2f′(2π3)∣=4\left|\frac{2}{f'(\frac{2\pi}{3})}\right| = 4.