Question
Question: Let $f(x) = \lim_{n\to\infty} \left( \frac{n^n (x+n)(x+\frac{n}{2})...(x+\frac{n}{n})}{n!(x^2+n^2)(x...
Let f(x)=limn→∞(n!(x2+n2)(x2+4n2)...(x2+n2n2)nn(x+n)(x+2n)...(x+nn))n1
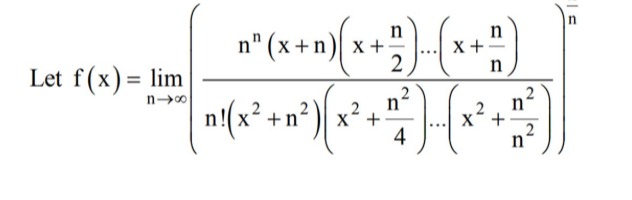
Answer
f(x)=exp{∫01ln1+x2t21+xtdt}
Explanation
Solution
Rewrite each product by factoring out the dominant n–terms and take logarithms. Express the sums as Riemann integrals in the limit n→∞. After cancellation and using Stirling’s formula, the limit becomes
lnf(x)=∫01ln1+x2t21+xtdt. Exponentiating gives the answer.
