Question
Question: Let $f(x) = \lim_{n \to \infty} \left( \frac{n^n(x+n)(x+\frac{n}{2})...(x+\frac{n}{n})}{n!(x^2+n^2)(...
Let f(x)=limn→∞(n!(x2+n2)(x2+4n2)...(x2+n2n2)nn(x+n)(x+2n)...(x+nn))nx, for all x>0. Then
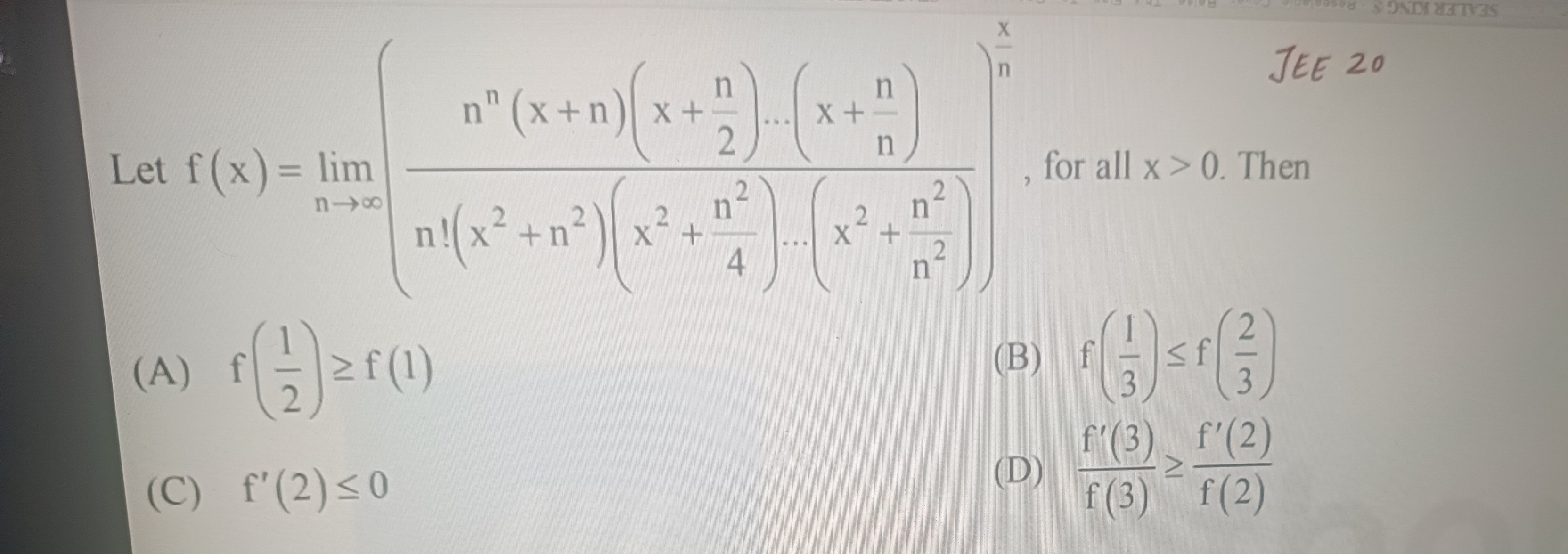
f(21)≥f(1)
f(31)≤f(32)
f′(2)≤0
f(3)f′(3)≥f(2)f′(2)
B, C
Solution
To determine the correct options, we first need to find an explicit expression for f(x).
Let the expression inside the limit be An.
An=n!(x2+n2)(x2+4n2)...(x2+n2n2)nn(x+n)(x+2n)...(x+nn)
We can rewrite the products as follows:
∏k=1n(x+kn)=∏k=1nkn(1+nxk)=n!nn∏k=1n(1+nxk)
∏k=1n(x2+k2n2)=∏k=1nk2n2(1+n2x2k2)=(n!)2(n2)n∏k=1n(1+n2x2k2)=(n!)2n2n∏k=1n(1+n2x2k2)
Substitute these into An:
An=n!(n!)2n2n∏k=1n(1+n2x2k2)nnn!nn∏k=1n(1+nxk)
An=n2n/n!n2n/n!∏k=1n(1+n2x2k2)∏k=1n(1+nxk)=∏k=1n(1+n2x2k2)∏k=1n(1+nxk)=∏k=1n1+n2x2k21+nxk
Now we need to evaluate f(x)=limn→∞(An)nx.
Let L=f(x). Then lnL=limn→∞nxlnAn.
lnAn=∑k=1nln(1+n2x2k21+nxk).
So, lnL=limn→∞nx∑k=1nln(1+n2x2k21+nxk).
This is a Riemann sum. Let t=k/n and dt=1/n.
lnL=x∫01ln(1+x2t21+xt)dt.
Thus, f(x)=exp(x∫01ln(1+x2t21+xt)dt).
Let g(x)=lnf(x)=x∫01ln(1+x2t21+xt)dt.
We can evaluate the integral using integration by parts.
∫01ln(1+at)dt=[tln(1+at)]01−∫011+atatdt=ln(1+a)−∫01(1−1+at1)dt
=ln(1+a)−[t−a1ln(1+at)]01=ln(1+a)−(1−a1ln(1+a))=(1+a1)ln(1+a)−1.
So, ∫01ln(1+xt)dt=(1+x1)ln(1+x)−1.
And ∫01ln(1+x2t2)dt=(1+x21)ln(1+x2)−1 is incorrect because the coefficient of t2 is x2, not x.
For ∫01ln(1+x2t2)dt, use u=ln(1+x2t2), dv=dt.
du=1+x2t22x2tdt, v=t.
∫01ln(1+x2t2)dt=[tln(1+x2t2)]01−∫011+x2t22x2t2dt
=ln(1+x2)−∫01(2−1+x2t22)dt=ln(1+x2)−[2t−x2arctan(xt)]01
=ln(1+x2)−(2−x2arctan(x)).
Let I(x)=∫01ln(1+x2t21+xt)dt=∫01ln(1+xt)dt−∫01ln(1+x2t2)dt.
I(x)=((1+x1)ln(1+x)−1)−(ln(1+x2)−2+x2arctan(x))
I(x)=(1+x1)ln(1+x)−ln(1+x2)+1−x2arctan(x).
Then g(x)=xI(x)=x((1+x1)ln(1+x)−ln(1+x2)+1−x2arctan(x))
g(x)=(x+1)ln(1+x)−xln(1+x2)+x−2arctan(x).
To analyze the options, we need g′(x)=f(x)f′(x).
g′(x)=dxd((x+1)ln(1+x))−dxd(xln(1+x2))+dxd(x)−dxd(2arctan(x))
dxd((x+1)ln(1+x))=ln(1+x)+(x+1)1+x1=ln(1+x)+1.
dxd(xln(1+x2))=ln(1+x2)+x1+x22x=ln(1+x2)+1+x22x2.
dxd(x)=1.
dxd(2arctan(x))=1+x22.
g′(x)=(ln(1+x)+1)−(ln(1+x2)+1+x22x2)+1−1+x22
g′(x)=ln(1+x)−ln(1+x2)+2−1+x22x2+2
g′(x)=ln(1+x)−ln(1+x2)+2−1+x22(x2+1)
g′(x)=ln(1+x)−ln(1+x2)+2−2
g′(x)=ln(1+x21+x).
Now, let's check the options:
Sign of g′(x):
g′(x)>0⟺1+x21+x>1⟺1+x>1+x2⟺x>x2⟺x(1−x)>0.
Since x>0, this implies 1−x>0⟹x<1.
So, g(x) (and f(x)) is increasing for 0<x<1.
g′(x)<0⟺1+x21+x<1⟺1+x<1+x2⟺x<x2⟺x(1−x)<0.
Since x>0, this implies 1−x<0⟹x>1.
So, g(x) (and f(x)) is decreasing for x>1.
g′(x)=0⟺x=1. This is a local maximum for f(x).
(A) f(21)≥f(1).
Since 1/2<1, and f(x) is increasing on (0,1), f(1/2)<f(1). So (A) is false.
(B) f(31)≤f(32).
Since 1/3<2/3 and both are in (0,1), and f(x) is increasing on (0,1), f(1/3)<f(2/3). So (B) is true.
(C) f′(2)≤0.
Since 2>1, and f(x) is decreasing for x>1, f′(2)<0. So (C) is true.
(D) f(3)f′(3)≥f(2)f′(2).
This is equivalent to g′(3)≥g′(2).
To compare g′(3) and g′(2), we need to check the monotonicity of g′(x).
g′′(x)=dxd(ln(1+x)−ln(1+x2))=1+x1−1+x22x=(1+x)(1+x2)1+x2−2x(1+x)=(1+x)(1+x2)1+x2−2x−2x2=(1+x)(1+x2)−x2−2x+1.
The denominator is positive for x>0. We need to check the sign of the numerator −x2−2x+1.
The roots of −x2−2x+1=0 are x=2(−1)2±4−4(−1)(1)=−22±8=−22±22=−1∓2.
The positive root is x=−1+2≈0.414.
Since the parabola −x2−2x+1 opens downwards, it is negative for x>−1+2.
Both x=2 and x=3 are greater than −1+2.
Therefore, g′′(x)<0 for x>−1+2. This means g′(x) is a decreasing function for x>−1+2.
Since 2<3 and g′(x) is decreasing in this interval, g′(2)>g′(3).
So, f(2)f′(2)>f(3)f′(3). Thus, option (D) is false.
Both options (B) and (C) are correct.
